今回の記事では体心立方格子の半径や充填率の求め方について
わかりやすく解説していきたいと思いますが、
その前に前回解説した面心立方格子の復習をしておきますね。
⇒面心立方格子の充填率の求め方
体心立方格子を理解するために面心立方格子の復習
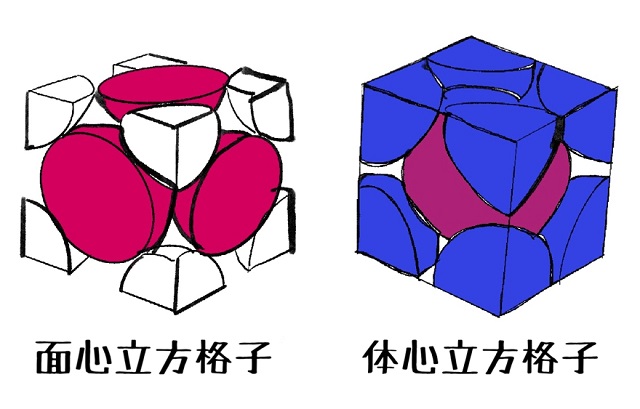
・面心立方格子は単位格子の中に原子が4つ入っていた
・原子半径r=$\sqrt{2} $a/4(4分のルート2a)
・1個の原子の周りに12個接している
・充填率は74.0%
です。
ちなみに面心立方格子の充填率は74%ですが、
これは他のものと比べても一番大きいです。
そもそも原子を球として立方体の中につめたと考えるので
どう頑張ってつめても74.0%が限界なのです。
では本題の体心立方格子について解説していきますね。
体心立方格子の半径や充填率はいくら?
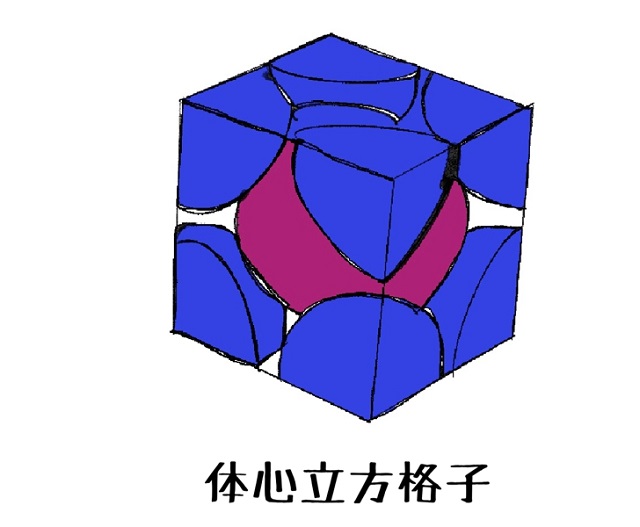
体心立方格子の体は立体の体です。

つまり立体の中心に王様がどんと構えている感じです。
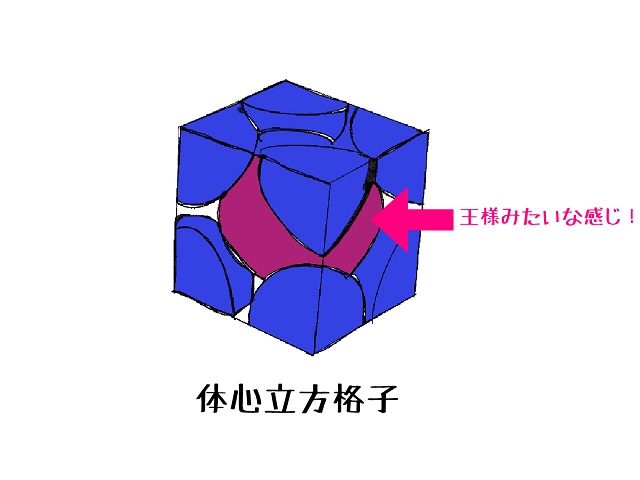
考えようによっては

桃の種みたいなものです。

つまり立体の中心に球体(赤色)がいます。
これが体心立方格子です。
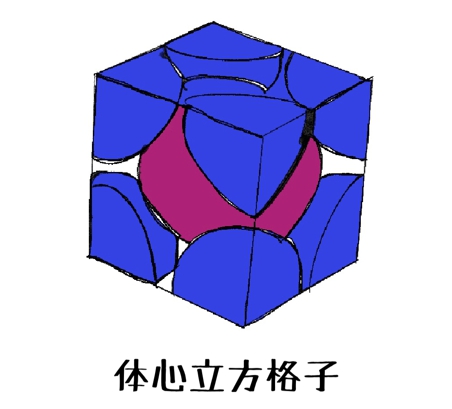
そして中心の赤色の球体の周りに青色で示している
8個の球体のカケラが存在します。
この立体の中に何個球体(原子)が入っていますか?
まず中心の赤色の球体が1個ありますね。
そして青色は赤色の8分の1に切られたものが8個存在しますね。
だから8分の1×8=1個
ということです。
よって赤色が1個と青色が1個=合計2個
2個の原子が立体の中に存在しているということです。
ちなみに面心立方格子は4個でしたね。
⇒面心立方格子の充填率の求め方
次に原子半径ですが、
考え方としては赤丸の中心を通ることを意識することです。
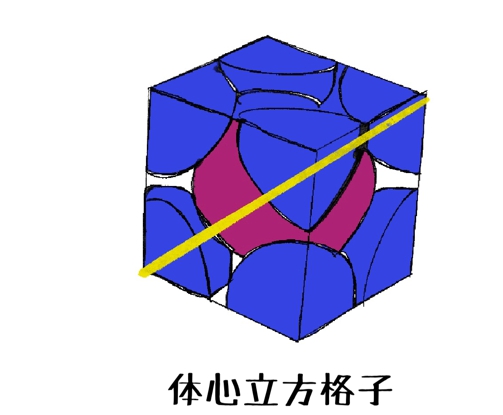
つまり、奥にある青色のカケラから中心の赤丸を通って手前の青色のカケラまで
直線を引きます(上記黄色の線参照)。
そして青色と赤色は接していますから、半径rは4つ分あります。
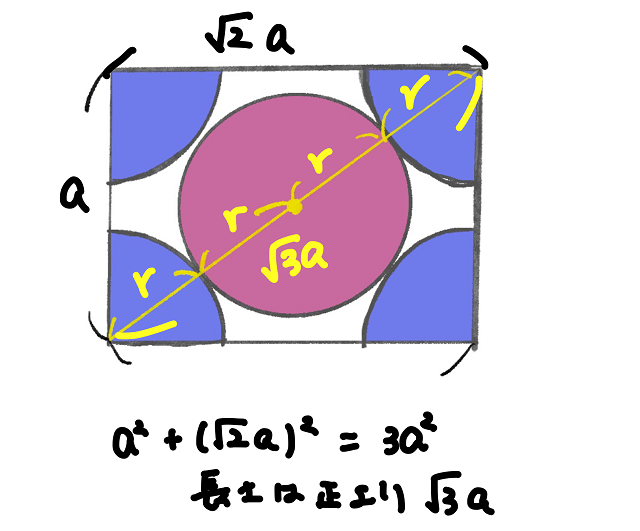
立方体の一辺をaとすると
対角線上に引いた黄色い線は上記画像のようになります。
三平方の定理より、縦が$a^{2} $、横が($\sqrt{2} $a$)^{2} $なので
斜辺は$a^{2} $+($\sqrt{2} $a$)^{2} $=$3a^{2} $
長さは正であり、負ではないから$\sqrt{3} $aとなり、これと半径4個(4r)と等しいから
4r=$\sqrt{3} $a
よって原子半径r=$\sqrt{3} $a/4
となります。
以上を利用して充填率を計算してみましょう。
充填率の式はこちらで解説しています。
⇒面心立方格子の充填率の求め方
充填率は2個の原子が立体の中に存在しているので
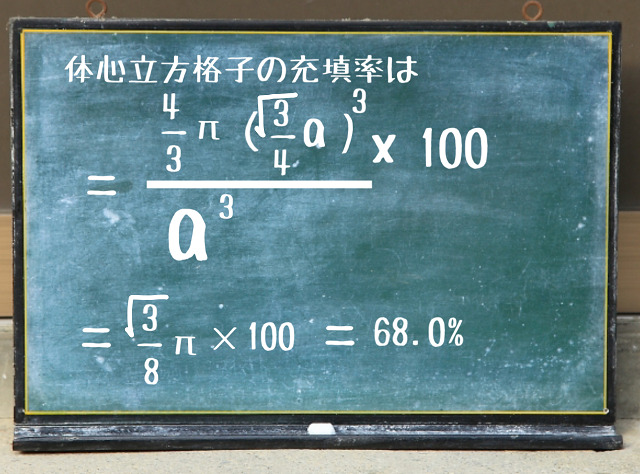
と体心立方格子の充填率は68.0%となります。
面心立方格子の充填率は74.0%でしたので、
面心立方格子より体心立方格子の方が中身はスカスカですね。

あと体心立方格子の接する原子数は8個です。
中心の赤い球体があって、この球体の周りに青色が8個くっついてますよね。
だから接する原子数は8個です。
面心立方格子の接する原子数は12個だったので
体心立方格子の方が4個少ないですね。
次の記事では六方最密構造について解説します。