面心立方格子の充填率の求め方

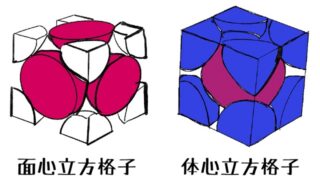
今回の記事では面心立方格子の充填率の求め方について
わかりやすく解説していきたいと思います。

面心立方格子は結晶格子の1つ

面心立方格子は結晶格子の1つです。
格子（こうし）は講師（先生の方）ではありません。
格子模様って知ってますか？

上記画像のように格子模様とは縦線と横線を組み合わせた模様のことです。
そして、結晶格子は立体であって、イメージとしては立方体です。

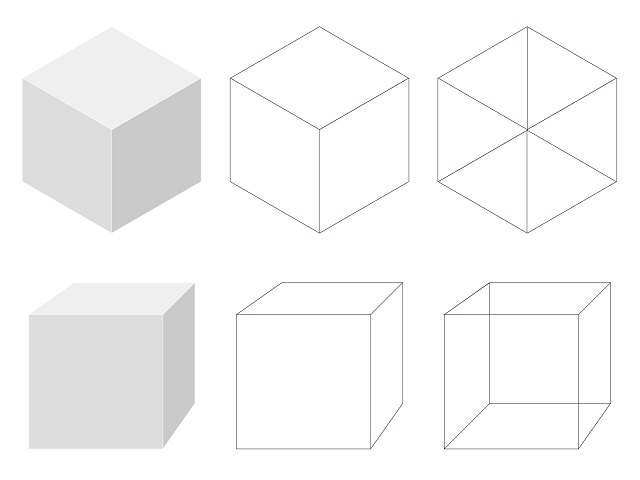
上記図のような形が立方体です。
なので結晶格子を勉強する時、「今私は立方体を勉強している」
と思っていただければと思います。

今回の記事テーマになっている面心立方格子は結晶格子の1つです。
なので面心立方格子も立方体です。

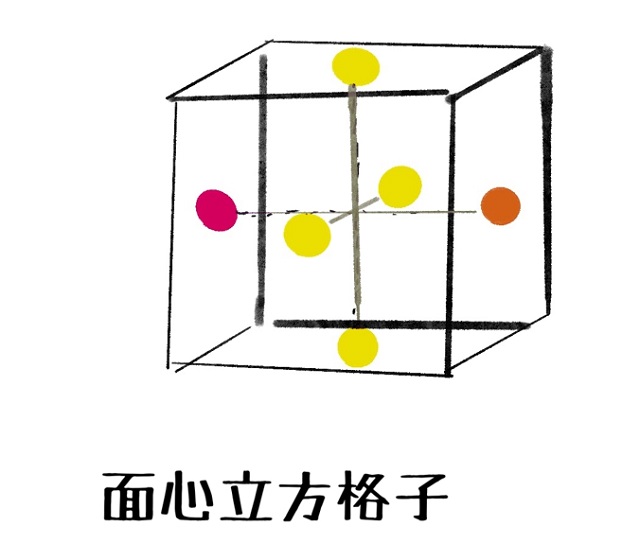
また、『面心』という言葉からもわかるように
『面』の中『心』に原子があるものを面心立方格子（上記図の赤丸参照）いいます。

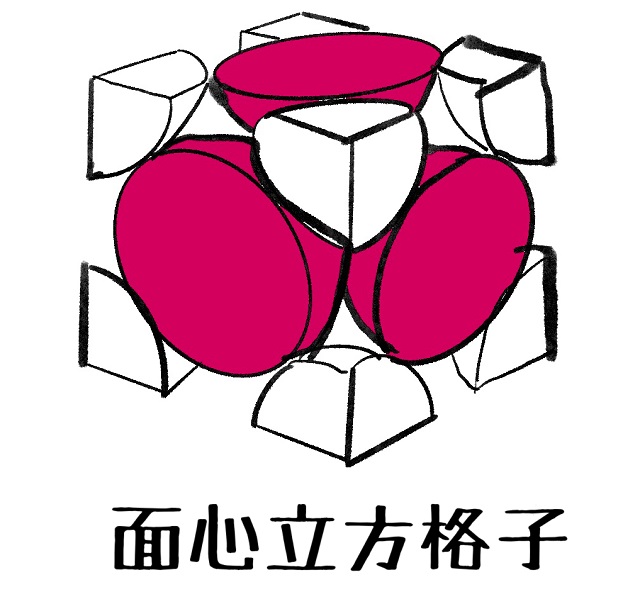
そして赤丸は『半分』になっています。
実際に原子を切るのは無理です。
面心立方格子の充填率を計算するための考え方になります。

たとえば金属の結晶を薄く切って顕微鏡で見てみても
立方体は見えません。

立方体というのは人間が都合のよいように作り上げただけのものです。
ある意味虚像ですよ。
実際には原子がひたすら積みあがっているだけです。

先日の雨の日。あれは本当は晴れの日の画像。加工。ここはその人の一部しか見せないから哀しみや辛さも表に出さないかもしれないし添加物にまみれた虚栄の嘘だけかもしれない。虚像も真実も隣合せ。想像で加工された世界。深入りせず浅く楽しむだけも良いし加工されてない君と出逢えればそれはそれね。 pic.twitter.com/8EGHBYTZ6X

— 祈織 (@EVs6o81) May 18, 2022

あくまで立方体というのは充填率などを計算しやすいように人間が
勝手に作り上げたものですからね。お間違いのないようにお願いします。

なので、上記図の隣にも同じ形をした立方体が存在しています。

半分に輪切りにされている赤丸と隣の立方体のやはり半分の赤丸が
合体することで、1つの球体が完成します。

立方体の上にも左隣にも右隣りにも下にも
同じ形の立方体が存在するってことですよ。

でもそうすると計算が難しくなるので
1個の立方体『だけ』みています。
そして1個の立方体『だけ』でみたら赤丸は球体の半分の大きさだってことです。

また、色を付けていませんでしたが
角にも球体のかけら（これから青色に塗ります）が存在しますね。

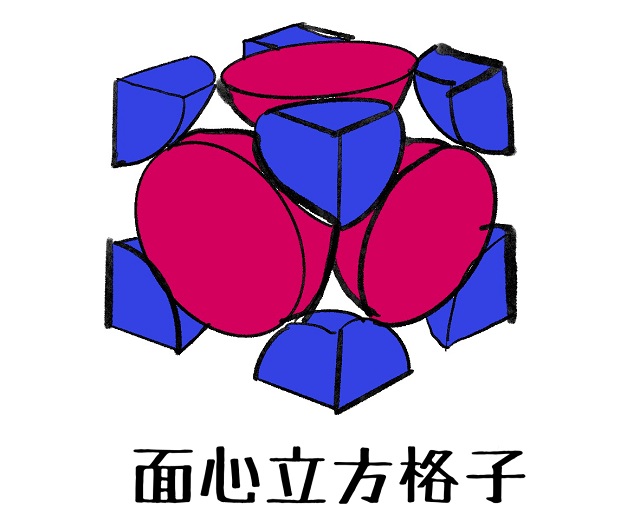
誤解しないでくださいね。
赤丸と青丸は1個になったら同じ球体ですよ。
ただ位置が位置がために色を変えています。
赤色と青色は1つの球体になったら同じ大きさ同じ形ですからね。

面心立方格子に存在する原子数は？

まず赤丸をご覧ください。
赤丸は2つ重なったら1個の球体になりそうですね。
なので、1つの立方体に存在する1つの赤丸は2分の1の大きさ（半分の大きさ）です。

この2分の1の大きさである赤丸は1つの立方体の中に何個ありますか？
3個ですか？違います。6個あります。
上記画像で見えている赤丸は3つですが、

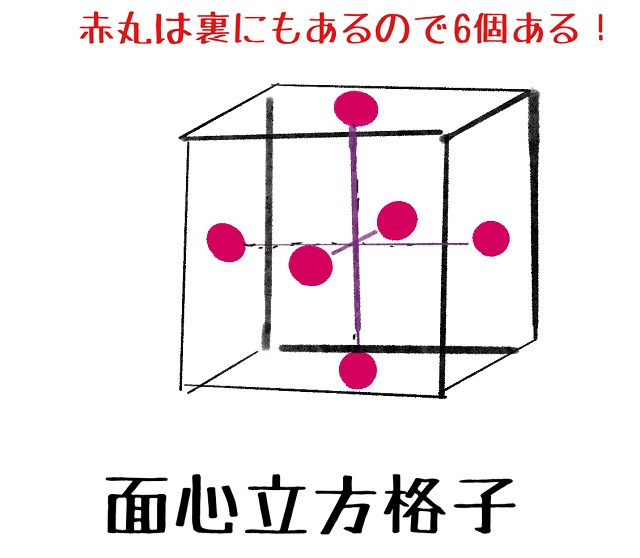
裏にも同じ数だけあるので実際には
1つの立方体の中に6個あります。
立方体の面はいくらつありますか？6つありますよね。

サイコロは1～6まで6つありますよね。
なので、立方体なら赤は6つあるはずです。

だから1つの立方体の中に2分の1の大きさの赤が6つあるから
2分の1×6＝3個の球体が存在することになりますね。

また青色はどうでしょう？
青色は立方体の頂点に存在します。
立方体の頂点に存在する青色は8つ揃って1個の球体になります。
青色の部分をよーく見てくださいね。4個揃って球体の半分になります。
だから8個そろったら1個の球体です。

だから青色は1個の8分の1です。
また立方体の頂点（角っこ）は8か所あるので
8分の1の青色が8か所あるので、1つの立方体の中に8分の1×8＝1個分の球体が存在します。

球体があるため、
1つの立方体の中に3個＋1個＝4個の原子（球体）が存在するということになります。

面心立方格子：原子半径は？

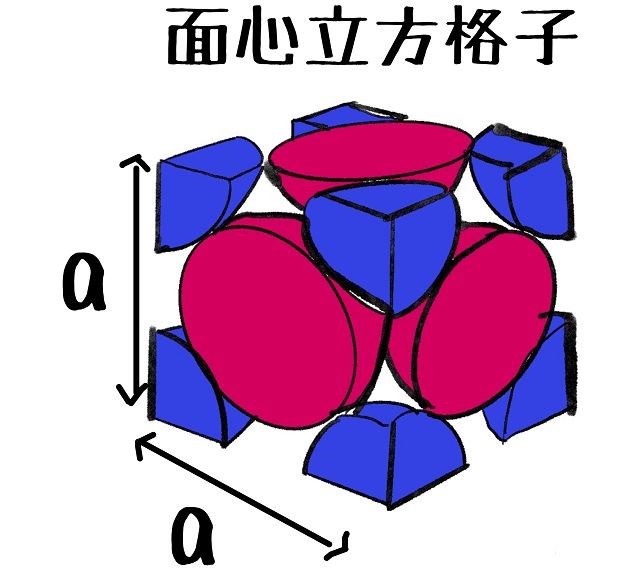
上記図は単位格子といいますが、
単位格子の1辺をaとします。

1辺をaとした場合、

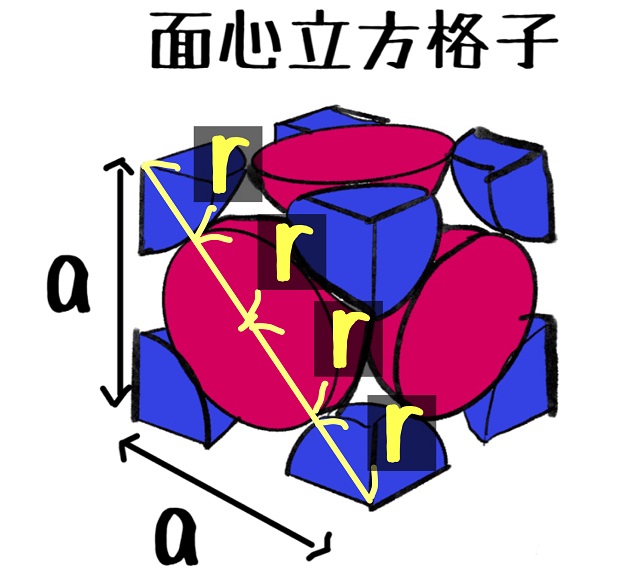
上記図のように頂点部分（青色の部分）を対角線上に黄色い線で結んでみると、、、
もちろん赤い中心も通ることになりますね。
なので、青い半径2つと赤い半径2つ（直径ということ）通るので
半径が4個分存在することがわかります。

この半径4個分というのは1辺がaの正方形の対角線なので、
三平方の定理を使って
$a^{2} $+$a^{2} $=（$4r）^{2} $
2$a^{2} $＝16$ｒ^{2} $
$a^{2} $＝8$ｒ^{2} $

rは長さなので必ず正なので計算を進めると
r=$\sqrt{2} $a/4（4分のルート2a）
となりますね。

面心立方格子：接する原子数はいくつある？

今度は接する原子数を数えていきましょう。
たとえば1個の原子を見た場合、
いくつ接しているのでしょう？

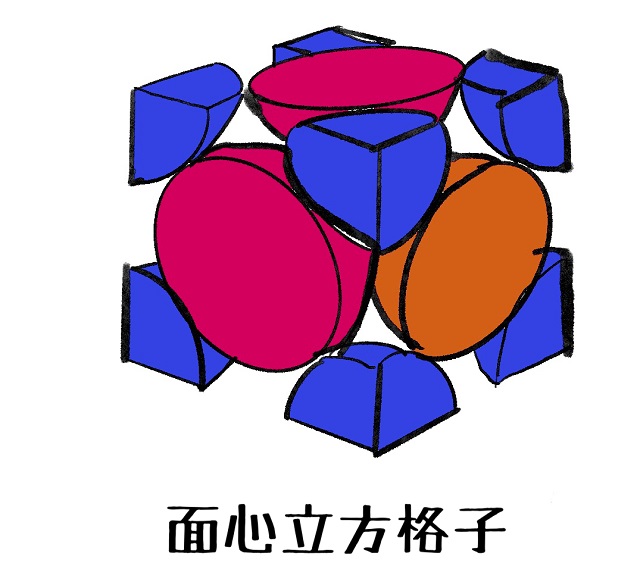
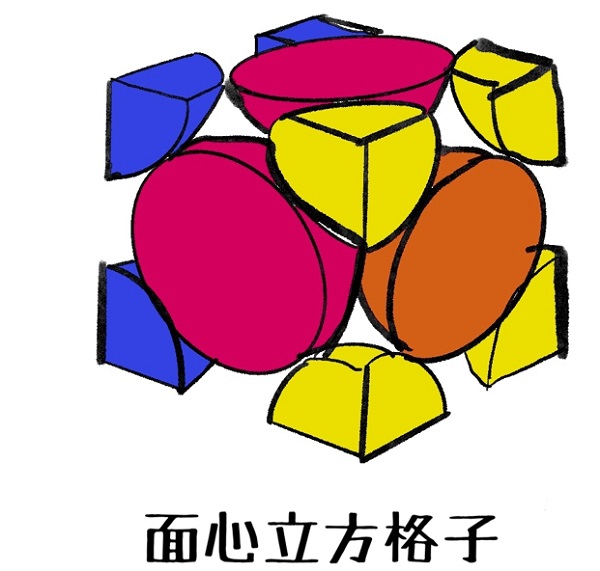
上記立方体の1個の色を茶色に変えますね。
茶色と赤色は立方体の中で接しています。
茶色を中心として赤色と接している数は4つです。

「2個じゃないの？」って思った方もいるかもしれません。

でも、赤色は裏側にもいますからね。
（上記図で黄色にした部分が元赤色の部分）
茶色と接することができる黄色（元赤色）は4個ありますよね。

次に茶色と接している青色の数はいくつあるでしょう？
4つありますよね。

青色を黄色く変えた部分と茶色は接しています。
だから4つですね。

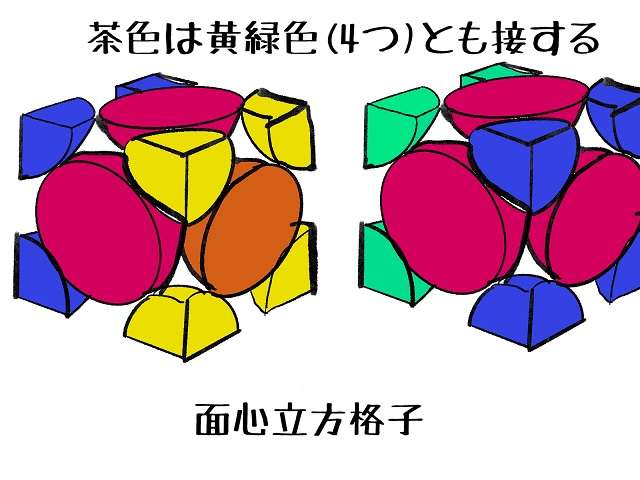
さらに、茶色の右側にも立方体があって接しています。
（上記画像の右側にある黄緑色部分と左側の茶色は接する）
黄緑色の部分は4個ありますね。

だから合計して、接する原子数は12個だとわかります。

面心立方格子：充填率

ということです。

ここまでわかったら充填率を計算しましょう。
充填率とはどれくらいつまっているか？を表すものです。

まず立方体の体積は$a^{3} $です。
1辺がaでしたからね。
それから球の体積は$\frac{4}{3} $$πr^{3} $です。
r（半径は）すでに計算で来てましたよね。

原子半径r=$\sqrt{2} $a/4（4分のルート2a）でしたね。

そんな球が4つ入っていますから充填率は、、、

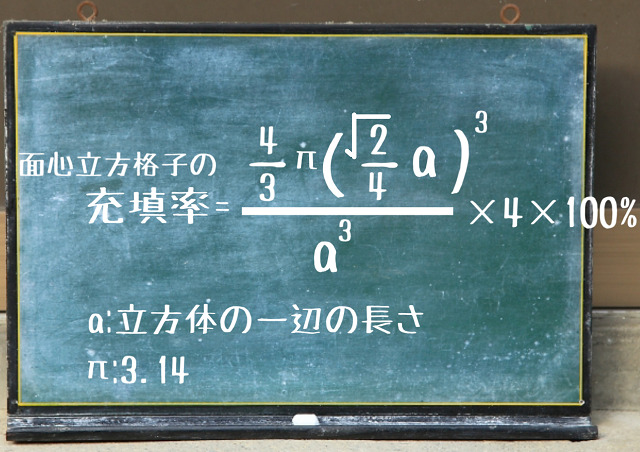
となります。

これを計算すると、
面心立方格子の充填率＝（$\sqrt{2}π $/6）×100％
＝約$\frac{1.414}{6} $×3.14×100％
＝0.740×100％＝74.0％
とわかります。

よって面心立方格子の充填率は74.0％だということです。

以上で解説を終わります。
「ちょっとわかりにくかったな・・・」
という方は、もう一度、この記事を見返していただければ
わかっていただけるのではないかと思います。
よろしくお願いします。

次の記事では体心立方格子について解説します。