塩化ナトリウムの結晶格子と密度の求め方についてわかりやすく解説

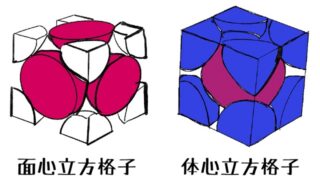
今回の記事では塩化ナトリウムの結晶格子と密度の求め方についてわかりやすく解説したいと思います。
これは以前に解説した内容の応用バージョンになりますので、
途中でよくわからなくなったら、以下の記事に戻ってみてください。
⇒面心立方格子の充填率の求め方
⇒体心立方格子の半径・充填率の求め方をわかりやすく解説

塩化ナトリウムの結晶格子

まずジャングルジムのような図を書いてみますね。

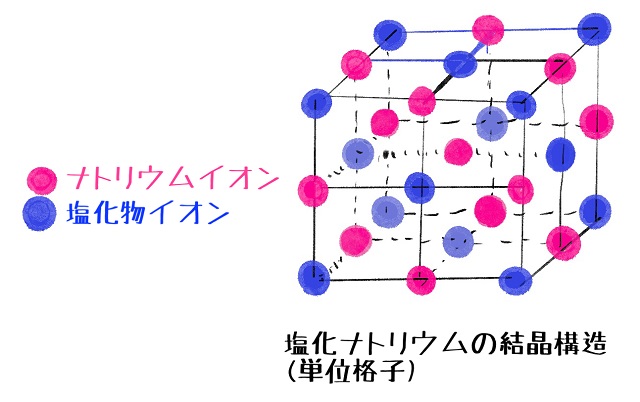
プラスのナトリウムイオンとマイナスの塩化物イオンが互い違いに並んでいます。
プラスとマイナスは引き付けあいますから
こうやってプラスとマイナスが交互に並ぶわけです。

逆に、プラスのナトリウムイオンの隣にプラスのナトリウムイオンがくることはありませんし
マイナスの塩化物イオンの隣にマイナスの塩化物イオンがくることもあります。

このジャングルジムみたいな形『全体』が単位格子です。
一番小さい立方体です。

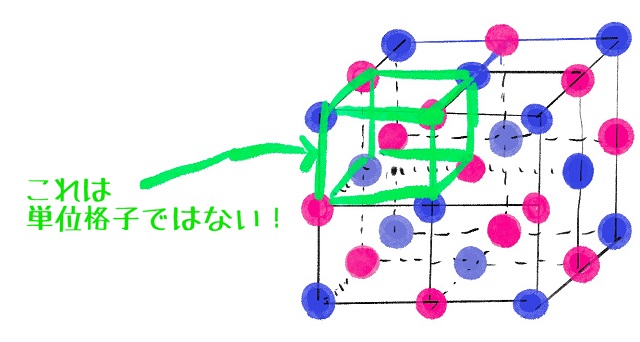
「あれ、もっと小さい立方体があるじゃないですか！
上記図の黄緑色の部分とか！」って思った方もいるかもしれませんね。
確かにこの黄緑色の立方体はものすごく小さいですよね。
でも、粒子は2種類あります。
ナトリウムイオンと塩化物イオンの2種類です。
粒子が2種類ありますから、2つの粒子を含んで、初めて単位格子です。

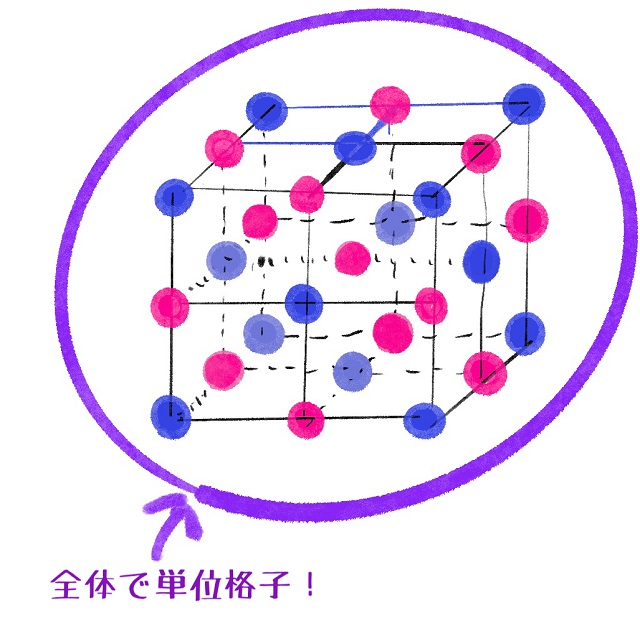
2つの粒子を含んで、『かつ』立方体になる最小こそが単位格子なので
上記画像が塩化ナトリウムの単位格子（最小単位）となります。
粒子が2種類（ナトリウムイオンと塩化物イオンのこと）あるので、
上記画像全体で最小単位です。

それから単位格子中にはナトリウムイオン、塩化物イオンがそれぞれ
4個ずつ存在します。

たとえば青色の塩化物イオンだけ見てみましょう。

青色だけ見ると面心立方格子と同じような並び方をしていますね。
⇒面心立方格子の充填率の求め方

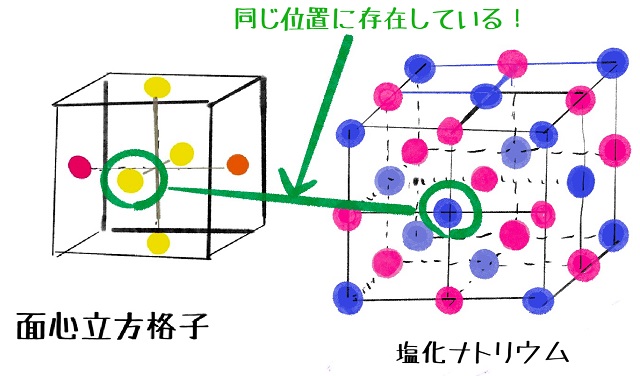
中心の青色と面心立方格子の中心の黄色が同じ位置に存在しています。
お互い正方形の中心にいますね。だから塩化ナトリウムの結晶格子の青色は
面心立方格子と同じです。

「では塩化ナトリウムの赤色はどうなの？違うの？」って思った方もいるかもしれませんね。
塩化ナトリウムの結晶格子は赤と青が互い違いになっているだけです。
だから1個ずらすと全部入れ替わります。
1個ずらすと正方形の真ん中に赤色の丸が来ます。

なので塩化ナトリウムの赤色だけを見ても面心立方格子と同じ構造になります。

ところで面心立方格子って1つの立方体の中に4個の原子（球体）が存在するんでしたね。
⇒面心立方格子の充填率の求め方

ということはナトリウムイオンは１つの立方体の中に4個存在することがわかります。
だって、赤色だけとか青色だけ見たら面心立方格子ということは
ナトリウムイオンだけで4個、塩化物イオンだけで4個
立方体の中に入っていることがわかるわけです。

入っているということです。

塩化ナトリウムの密度はいくら？

塩化ナトリウムの密度を求めるのに必要な数値を挙げていきますね。

です。
⇒原子量と質量数の違いについてわかりやすく解説

です。

アボガドロ数は$6.0\times {10}^{23}$です。
⇒アボガドロ数とは？わかりやすく解説

ところで密度の単位はg/$c{m}^3$です。
言い換えると密度とは1立方センチメートル当たり何グラムか？を表す数字のことです。
つまり、グラムを立方センチメートルで割り算すればOK。

この単位になるように塩化ナトリウムの密度を求めるための計算式を立てていきましょう。

ナトリウムの原子量が23ということです。
1モル集めると23グラムということですね。
⇒モル（物質量）とは？わかりやすく解説

ということは原子量23をアボガドロ数$6.0\times {10}^{23}$で割れば（23÷$6.0\times {10}^{23}$）
ナトリウム1個の重さという意味になりますね。

同様に塩素の原子量は35.5なので、$6.0\times {10}^{23}$で割れば（35.5÷$6.0\times {10}^{23}$）
塩素1個の重さになりますね。

もしかしたら「今回のはナトリウムイオンや塩化物イオンですよね？
塩素やナトリウムは原子でしょ？違いますよね？」
って思った方いるかもしれませんね。

でも、電子ってほとんど重さがありません。
電子の大きさは陽子や中性子の大きさの1840分の1くらいの質量しかありません。
だからイオンになってもナトリウムイオンなら23だし
塩化物イオンなら35.5であることに変わりありません。

これはこちらの記事で詳しく解説しています。
⇒原子の構造について図を使ってわかりやすく解説

ここまででナトリウムイオン1個と塩化物イオン1個を出しましたが、
これらが4個ずつあるのでした。
なので4倍しましょう。

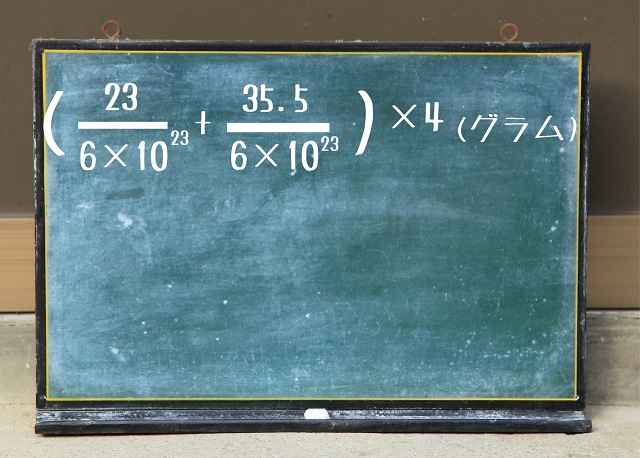
これで単位格子中に含まれるナトリウムイオンと塩化物イオンの重さ（グラム）が計算できました。

上記数字を立方センチメートルで割ればよいわけですね。

では1辺はどれくらいでしょうか？

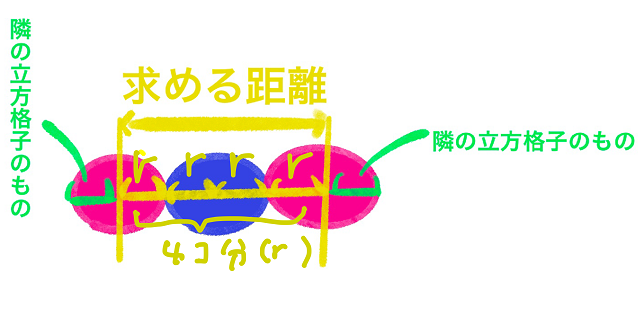
赤色と青色の球を立方体の配列に従って並べてみました。
黄色い線で中心から中心に線を引きます。
赤色の球の半分は隣の立方格子のものです。

なので赤色の中心から赤色の中心までが1辺の長さになります。
すると、青色の半径が2つ分と赤色の半径が2つ分ありますね。

また、

でしたから、
$1.0\times {10}^{-8}$㎝×2＋$1.8\times {10}^{-8}$㎝×2＝$5.6\times {10}^{-8}$㎝となりますね。
密度の単位はg/$c{m}^3$と$c{m}^3$なので$5.6\times {10}^{-8}$㎝を3乗します。

よって、（$5.6\times {10}^{-8}$${）}^3$$c{m}^3$となりますね。

先ほどのグラムを$c{m}^3$で割ると、

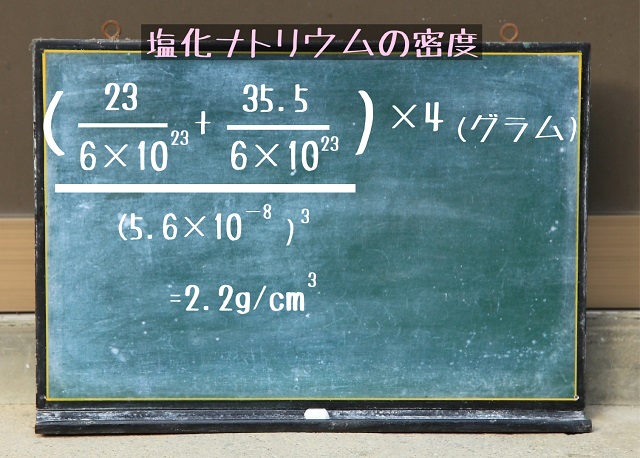
約2.2g/$c{m}^3$
となります。

食塩です
塩化ナトリウムです
NaClです
式量58.44です
密度は2.18g/cm^3です
融点は1074Kです
沸点は1686Kです

— 食塩 (@sho_ku_en) February 5, 2018

以上で解説を終わります。