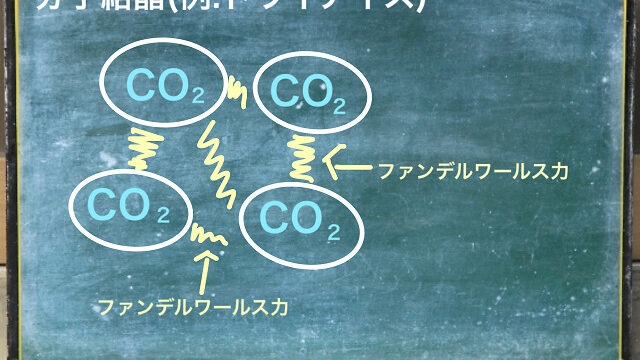
今回は原子というものすごく小さな粒の構造がどうなっているのか?解説します。
すべての物質は原子というものすごく小さな粒が無数に集まってできています。
あなたの前にある机もパソコンも、
猫を飼っている方なら愛猫を見てください。
すべて最小単位まで切り詰めてみていくと原子に行きつきます。
では原子ってどれくらい小さいと思いますか?
原子の直径は1×$10^{-10} $です。
といわれてもおそらく「???」でしょう。
ピンとこないと思います。
たとえばあなたの身長が160㎝だったとしましょう。
身長160㎝の人から見た原子という小さい粒を
単純にどちらも掛け算して大きくしてみます。

もし原子をアリの大きさまで拡大したとします。
では身長160cmの人を同じ割合で大きくしたらどれくらい大きくなると思いますか?

160㎝の身長がある人を原子をアリの大きさまで拡大したのと同じ倍率で拡大したら
地球の大きさと同じ大きさになります。
身長が160㎝の人が見た原子というのは
地球から見たアリくらいの大きさだということです。
原子の大きさ:身長160㎝の人=アリの大きさ:地球の大きさ
ということです。
そんなめちゃくちゃ小さな粒が原子です。
そして原子こそがすべての物質を構成する最小単位です。
ではこの原子の構造はどうなっているのでしょう?
原子の構造をわかりやすく図で説明します
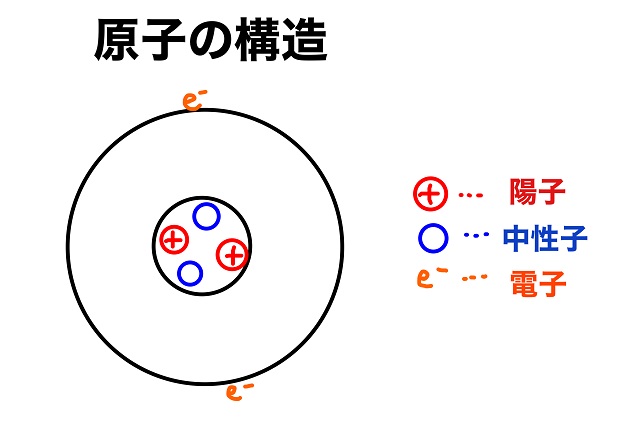
原子の構造=原子の中身を見るということです。
原子の中にはもっと小さい素粒子というさらに小さな粒が入っています。
・陽子(プラスの電気を持った粒)
・電子(マイナスの電気を持った粒
・中性子(プラスもマイナスも電荷を持たない)
という3種類の粒が入っています。
まず原子の中に含まれる3種類の粒は
どこにあるのか?勉強していきましょう。
原子は以下の図のような二重層構造でできています。
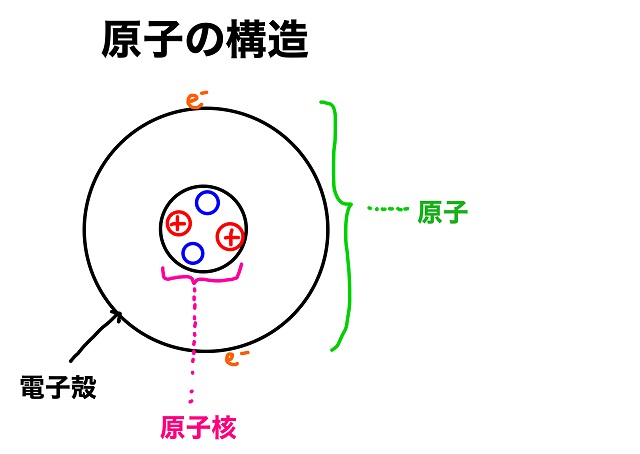
上記円の中でピンク色の範囲の部分を『原子核』といいます。
原子核=原子の核になる部分ということです。
この原子核の中には陽子というプラスの電気を持った粒と
中性子という電気を持たない粒が存在します。
この原子核の周りをマイナスの電気を持った電子が飛び回っています。
電子が飛び回っている空間を電子殻(でんしかく)といいます。
電子殻の殻と原子核の核は漢字が違うので要注意です。
以上を全部含めて『原子』といいます。
上記図では原子核の半径と電子殻の半径の比率は1:2程度ですが、
実際には原子核が仮に10円玉1個分だとすると原子全体というのは
東京ドーム1個分くらいの大きさになります。

つまりものすごく小さいところに陽子と中性子がつまっていて
そのものすごく遠いところを電子が飛び回っているというのが
原子の構造なんです。
先ほど身長160㎝の人から原子は地球から見たアリだと説明しましたが
原子核はさらにその10万分の1くらいの大きさです。
ですから、原子の構造(中身)はスカスカだということです。
原子の構造の特徴
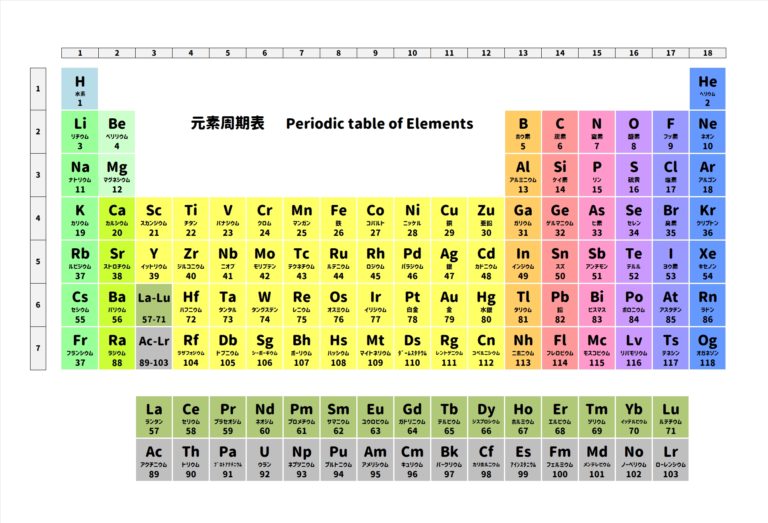
・陽子の数は原子番号(周期表の並び順のこと)と電子の数と同じ
(陽子数=原子番号=電子数)
⇒プラスの数とマイナスの数が同じだから電気的に中性という特徴がある
・中性子の数は不規則(一定ではない、2個になったり3個になったり・・・)
・陽子や中性子は軽いが0ではない程度の重さを有するが
電子は陽子や中性子と比べて、ものすごく軽い
| 質量 | 電荷 | |
|---|---|---|
| 陽子 | 1と仮定 | +1 |
| 中性子 | 1と仮定 | 0 |
| 電子 | 約0 | ー1 |
上記表で電荷ですが、陽子は+1で電子はー1になっていますね。
単位は何でしょう?
単位は電気素量(でんきそりょう)といいます。
1モル集めると1F(ファラデー)になります。
⇒モル(物質量)とは?わかりやすく解説
電気素量は$1.6×10^{-19} $C(クーロン)です。
1モルは$6.02×10^{23} $なので、
$6.02×10^{23} $×$1.6×10^{-19} $=約96500(C)となり、
これを1F(ファラデー)とおきます。
つまり、96500C(クーロン)=1F(ファラデー)となります。
こんな感じなので、1モル集めて1Fとして計算問題を解いていくのが楽です。
それから、電子は中性子や陽子の重さと比べてものすごく軽いといいましたが、
電子の大きさは陽子や中性子の大きさの1840分の1くらいの質量しかありません。
つまり電子は陽子や中性子を1としたとき、1840分の1の質量しかないということです。
陽子と中性子はほぼ同じ大きさ重さなのです。
だから上の表では電子の質量を約0と書きました。
では、陽子や中性子の質量の単位って何でしょう?
原子質量単位といいます。
ピンと来ないかもしれませんね。
1モル分集めたら陽子が1gという計算になります。
⇒モル(物質量)とは?わかりやすく解説
1モルは$6.02×10^{23} $です。
そして陽子や中性子1個の重さって$1.67×10^{-24} $gです。
なので、$6.02×10^{23} $×$1.67×10^{-24} $=約1gとなります。
ですから、1モル集めたら1gという理解で大丈夫だということです。
たとえると、体重が100㎏の人が60gのお餅を食べた程度の話です。
体重が100㎏の人が陽子や中性子でお餅が電子の重さです。
体重100㎏の人が60gのお餅を食べた後、
体重を測っても重さに変化がないでしょう。
つまり、電子は無視できる程度の重さしかないということです。
原子1個の重さは電子の数は影響せず、
陽子と中性子の合計数で決まってくるということです。
質量数=陽子の数+中性子の数
ということです。
質量数というのは原子1個の重さを決める数字のことです。
たとえば、先ほどの図

陽子数が2個なので原子番号は2番ということですね。
周期表からHe(ヘリウム)だとわかります。

この場合、陽子の数も中性子の数も2個なので合計4個だから
質量数は4ということです。
陽子と中性子の数の合計がいくつあるかが、
原子1個の重さを決める数字になります。
ナトリウムを例に原子の構造について考えてみよう

ナトリウム(Na)は原子番号が11で質量数が23です。
質量数は重さです。
なのでナトリウムを1モル集めると23g(グラム)になるということです。
ところで
原子番号とは原子核中に含まれる陽子の数のことです。
なので、
原子番号=陽子数
です。
また陽子数=電子数
でもあります。
先ほど電荷について解説しましたが
陽子は+1で電子はー1でしたね。
原子は電気的に中性です。
中性とは電気が0ということです。
もし電気が0でないなら、それはイオンです。
プラスの数とマイナスの数がもし違ったら
たとえば陽子の数の方が大きいなら、全体としてプラスですし
電子の方が多かったら全体としてマイナスです。
電気を持ってしまいます。
もし電気をもったらそれはイオンといいます。
原子というのは電荷を持ったらいけません。
なので、プラスの陽子とマイナスの電子は同じ数でないといけません。
なので、
原子番号=陽子数=電子数
です。
よってナトリウムの場合、
原子番号が11なので陽子数も電子数も11個だとわかります。
次に質量数。
質量は電子はほぼ0でしたね。
つまり質量があるものは陽子1と中性子1だけです。
よって
質量数=陽子数+中性子数
となります。
しかも陽子数は1で中性子数は1と同数で
個数がそのまま質量数という重さになります。
ここでナトリウムの質量数は23とわかっています。
ということは陽子数+中性子数=23となるわけですね。
全部で23個あれば1モル集めて23gです。
だって1個は1モル集めると1gですからね。
ということはナトリウムの場合、質量数が23で陽子数(=原子番号)は11だから
中性子数=23ー11=12となりますね。
こんな感じで質量数と原子番号が分かれば中性子数も求めることができます。
以上のことが理解できたら、
次に同位体について学習しましょう。
⇒同位体とは?炭素を例に分かりやすく解説