今回の記事では加速度とは何か、わかりやすく解説します。
加速度とは何か、わかりやすく説明
加速度のお話をする前に加速度運動について解説します。
加速度運動とは何か?
加速度運動とは何か?というと
『速度が変化する運動』のことです。
例えば以下の表をご覧ください。
| t【s】 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| v【m/s】 | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
上の表でt【s】は時刻で単位はs(秒)です。
v【m/s】は速度で【m/s】ははメートル毎秒を表します。
時刻が0から6と変化していった時に
時刻ごとに速度が0、2、4、6、8、10、12と変化しているような物体があるとしましょう。
このとき速度が0、2、4,6,8,10,12と
時刻を追うごとに変化しています。
こんな感じで時刻が変化するたびに速度が変化するものを加速度運動といいます。
速度が変化する運動のこと
です。
加速度とは?
単位時間当たり速度がどれだけ変化するかを表したもの。
単位時間は通常秒を使う。
です。
ところで1秒ごとに物体の速度を調べていった結果を
記載しているのですが、1秒ごとにどれだけ速度が
変化しているでしょうか?
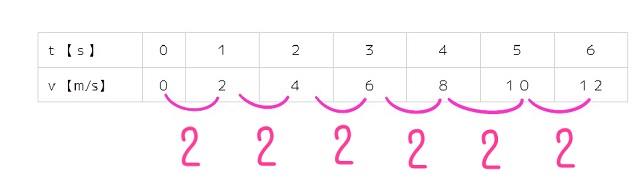
最初の0から1秒の間、速度が0から2、
つまり2だけ増えていますね。
次の1秒間はどうでしょう?
時刻1から2で速度も2から4とやはり2だけ増えています。
速度の変化量が2です。
同様にそれぞれえの区間、2ずつ速度が変化しています。
1秒ごとに速度が2ずつ変化しているような場合、
この運動の加速度は2であるといいます。
この2という値のことを加速度といいます。
もう1つ例を挙げますね。
| t【s】 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| v【m/s】 | 12 | 10 | 8 | 6 | 4 | 2 | 0 |
上記の場合はどうでしょうか?
時刻0のときはプラス12m/sだったものが1秒後の時刻1では
10m/s、さらに1秒たった時刻2には8とどんどんプラスの速度が減っていっています。
このような場合も速度が変化しています。
だから加速度運動です。
ではどれだけ1秒当たり変化しているのでしょう?
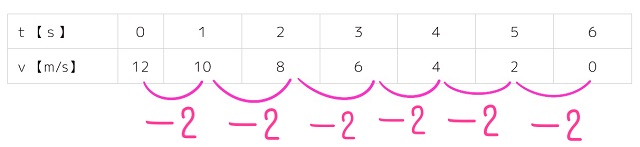
見てわかると思いますが、
最初の時刻0から1までの1秒間には速度が12から10と2減っています。
この場合、速度の変化量は2減ってますから―2になります。
同様に時刻1から2までの1秒間、
速度は10から8と2減っていますから速度の変化量はマイナス2になります。
といった感じで、それぞれ1秒当たり-2ずつどの区間でも変化しています。
この場合はこの運動の加速度は-2であるといいます。

上記の場合の加速度は+2。

上記の場合の加速度はー2。
同じ2でも符号が違えば運動の様子がまったく違ってきます。
ここまでの解説でなんとなくわかっていただいたと思います。
加速度というのは前回解説した変位や速度と同じで向きを持つ量になります。
⇒速度と速さの違い【物理】
先ほどの例をx軸上を運動するものとして考えてみますと、

上記の場合、
0、1、2・・・と時間の経過とともに
速度が0、2、4・・・と増えていきます。
これはどういうことでしょう?
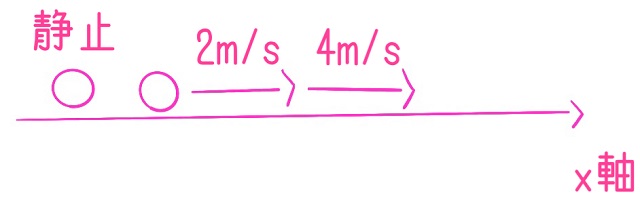
最初止まっていたものが
右向きにプラスの向きに動き始めて
1秒後には2m/sになり、時刻2には 4m/sと
どんどん正の向きに速くなっていっているわけです。
そういうのが加速度が2の運動です。

一方で加速度がー2の運動はどうでしょう?
はじめ速度は+12m/sです。
プラス12ですからX軸で正の向き、右向きに運動しています。
ところが+10m/s⇒+8m/s⇒+6m/sと
プラスの向きに動いていますが、
遅くなっていきます。
やがて6秒後には0m/sとなり止まってしまいます。
この場合、加速度の向きは左向きに2という値になります。
以上をまとめますと、
速度が変化する運動のこと
そして
単位時間当たり速度がどれだけ変化するかを表したもの。
単位時間は通常秒を使う。
なので1秒あたり何m/s速度が変化するかを表すのが加速度
です。
ここまでわかったらもう少し応用的な解説をさせていただきますね。
まず時刻をtとします。
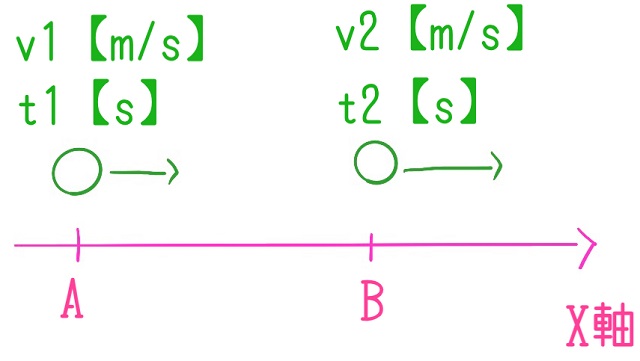
そして時刻がt1【s(秒)】のときにA点に物体がいて
速度がv1【m/s】だったとしましょう。
これがX軸上を運動して時刻がt2【s】のときに(B点)速度が変化してv2【m/s】に
なったとしましょう。
v1からv2に速度が変化した時、
AB間の加速度を考えてみましょう。
加速度を出す前にAからBに移動する過程における速度の変化が
どれだけあったかを考えていきます。
速度はv1からv2に変化していますから、
変化後の速度v2から変化前の速度v1を引いてあげれば
速度変化の量になります。
つまり
v2ーv1【m/s】
(変化した速度の量のこと)
となります。
この変化した速度の量(v2-v1【m/s】)を
変化に要した経過時間で割ってあげれば加速度が出てきます。
AB間の(平均)の加速度は速度変化(v2-v1【m/s】)を
経過時間で割ってあげます。
経過時間は時刻がt1からt2になったときですから、
後の時間t2から最初の時間t1を引いて
(t2ーt1【s】)となります。
よって
加速度(a)=速度変化÷経過時間
=(v2ーv1)÷(t2ーt1)【m/$s^{2} $】
となります。
加速度は小文字のaを使います。
物理でaが出てきたら加速度だと考えてください。
またもう1つ重要なことがあります。
加速度の単位ですがm/$s^{2} $となります。
読み方はメートル毎秒の2乗と書いて『メートル毎秒毎秒』となります。
どうして加速度はm/$s^{2} $という単位になるのでしょうか?
加速度というのは速度変化を時間で割ったものです。
速度変化の単位は速度と同じm/sです。
これを時間(秒)で割ります。
だからm/s÷sとなり
=m/s×1/sとなります。
つまりm/$s^{2} $となるわけですね。
だから加速度の単位はm/$s^{2} $となります。
では問題を解いて、加速度について理解できたか?
確認していきましょう。
加速度とは?理解できたか問題で確認
X軸上を運動する物体の速度が5秒間で3msから18m/s
に変化したとする。この物体の加速度はいくらになる?
初め物体は3m/sで運動していて
5秒後に18m/sになっています。
このとき5秒間で速度はどれだけ変化したでしょうか?
速度変化は3m/sから18m/sに変化した場合、
変化後の速度18m/sから変化前の速度3m/sを引けば速度変化になります。
なので18ー3=15m/sが速度変化です。
この速度変化15m/s、これは5秒間で変化していますから
時間で割ってあげて加速度a=15÷5=3m/$s^{2} $となります。
よろしいですか?
5秒間に15だけ速度が変化しているから1秒あたり3m/sずつ
速度が変化しているということです。
X軸上を運動する物体の速度が時刻5【s】のとき3m/sで
時刻8【s】のとき―6m/sだったとする
この区間の加速度はいくらになる?
問題(2)は時刻が5s(秒)のとき
正の向きに3m/sだったものが
なんと8秒のときには逆向き(負の向き)に―6m/sになってしまったというパターンです。
こんな場合でもビビる必要はありません。
先ほど解説した
加速度(a)=速度変化÷経過時間
=(v2ーv1)÷(t2ーt1)【m/$s^{2} $】
の公式に当てはめればOKです。
移動後の速度から移動前の速度を引いたのが速度変化です。
移動後の時刻8秒の速度-6m/sで
移動前の時刻5秒の速度3m/sを引いたものが速度変化です。
なので、-6ー3=-9m/s
これを経過時間で割ってあげれば加速度になります。
経過時間は5から8に時刻が変化してますから
遅い方の時間8から早い方の時間5で
8-5=3秒。
よって加速度a=―9m/s÷3s=-3【m/$s^{2} $】となります。
つまり、はじめX軸上で右だったものが
今度は左側に移動してしまった場合、
加速度が負(左向き)になってしまったってことです。
以上で加速度とは何か?についての解説を終わります。
もし速度についての復習をしたい方がいましたら
こちらをご覧ください。
⇒速度と速さの違い【物理】














