電離定数を使ったpHや電離度の求め方をわかりやすく解説

といった解説をします。

電離定数がらみの問題が解けない方は必読の内容になっていますので
ぜひ最後までご覧ください。

電離定数とは？酢酸を例にわかりやすく解説

以前の記事で酢酸は100人の兵隊さんが戦地に行くけど、
99人の兵隊さんは臆病だから戻ってくるみたいな話をしたことがあります。

そして酢酸の場合、以下の式が成り立ちますよね。
$CH_3COOH $⇔$CH_3COO^{ー} $＋$H^{＋} $

で、上記式について電離定数が定義できます。
電離定数はKaと書くことが多いのでKaとしますね。

Kaのaですが、酸は英語でacidといいます。
酢酸は酸性ですよね。
なので、Kaとaを付け加えているのです。

で、電離定数の作り方ですが、左辺が分母、右辺が分子にきます。
また、【】はモル濃度（mol/L)です。

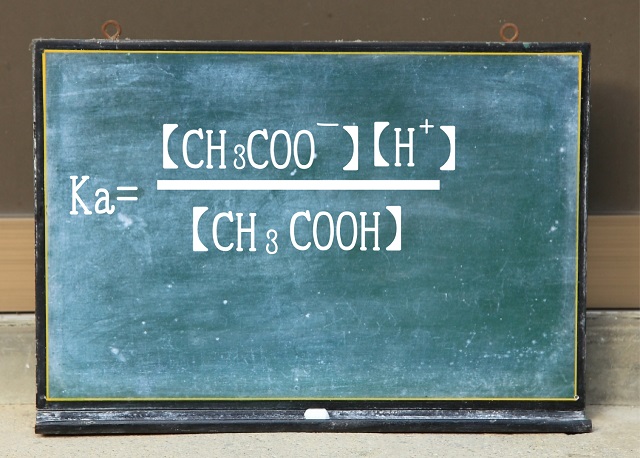
上記式、どこかで見たことがないですか？
覚えてますか？平衡定数と同じですよね。

そして酸塩基における平衡定数を特に電離定数といいます。

$CH_3COOH $⇔$CH_3COO^{ー} $＋$H^{＋} $

どういうことか？というと上記式のようにイオンに電離しますよね。
イオンに分かれることを電離といいます。
なので電離反応における平衡定数なので、特に電離定数と呼ぶわけです。
あくまで電離定数は平衡定数の一種です。
なのでもしかしたらあなたはすでに学習済みの内容なのかもしれませんね。

ですから平衡定数を思い出してくださいね。
平衡定数ってなんでしたっけ？
温度が変わらなければ一定でした。

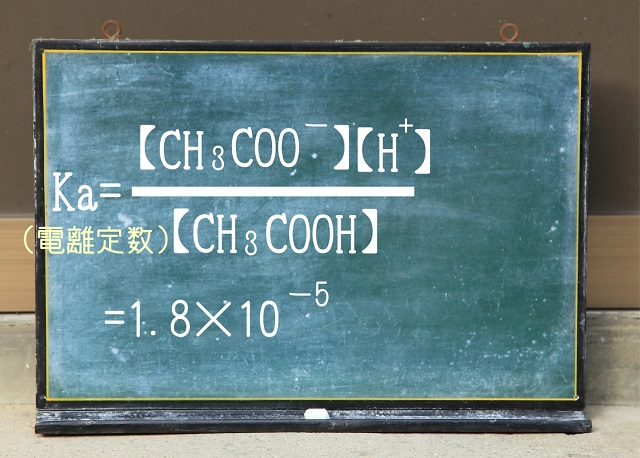
たとえば酢酸の電離定数は1.8×$10^{-5} $(mol/L)です。
$10^{-5} $というのは10万分の1です。
だから相当小さいです。

また酢酸の電離定数は1.8×$10^{-5} $(mol/L)と単位がmol/L
となっていますね。

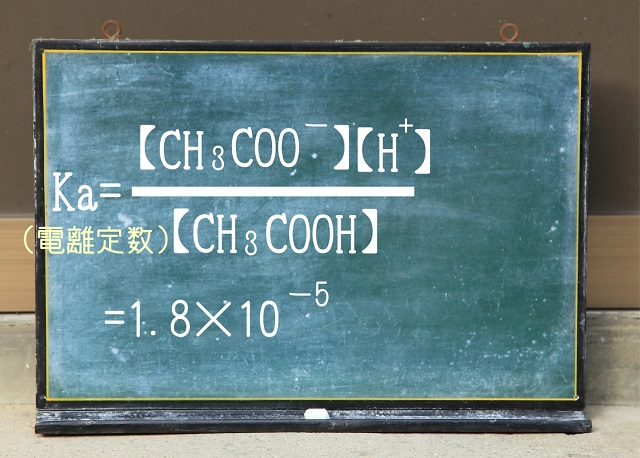
上記式をご覧ください。
分子に【$CH_3COO^{ー} $】×【$H^{＋} $】と２つありますね。
どちらも単位はmol/Lです。
つまり分子の単位は(mol/$L)^{2} $です。
これに対して分母は【$CH_3COOH $】１つなので単位はmol/Lです。

ということは(mol/$L)^{2} $÷mol/L＝mol/L
となるから電離定数の単位はmol/Lとなるわけですね。

また酢酸の電離定数1.8×$10^{-5} $(mol/L)は25℃のときに成り立ちます。
電離定数は平衡定数の一種ですから、温度が一定のときに一定の値になります。

もしかしたら誤解している方がいるかもしれませんが、
アルカリ性の溶液を入れると中和しますよね。酢酸は弱酸性ですから。
でも、アルカリ性を入れて中和しても温度が一定なら電離定数は一定です。
アルカリ性で中和しても25℃なら酢酸の電離定数は1.8×$10^{-5} $(mol/L)です。

もちろん酢酸単独でも25℃と温度がいっていなら電離定数1.8×$10^{-5} $(mol/L)です。
こんな感じでどんな状況でも酢酸だけをとったら温度さえ変わらなければ
必ず成り立つように動いているんです。

さて、電離定数について解説したので
電離定数を利用してｐHや電離度を求める計算問題を
一緒に解いていきましょう。

電離定数を利用してpHや電離度を計算してみよう

まずは式を書きましょう。
$CH_3COOH $⇔$CH_3COO^{ー} $＋$H^{＋} $
酢酸が一部電離します。
実際にはちょっとしか右辺に行きません。

αを電離度とします。
電離度とはどれくらい電離するか？割合のことです。
最初の$CH_3COOH $の濃度をC(mol/L）としましょう。
問題文に0.18mol/Lとなっていますが
公式的なものを作りたいのでここではC（mol/L)とおいておきますね。

すると最初は
$CH_3COOH $⇔$CH_3COO^{ー} $＋$H^{＋} $
の式において

となりますね。

そしてαという割合だけ電離します。

となりますね。

$CH_3COOH $⇔$CH_3COO^{ー} $＋$H^{＋} $
全体を１としたらαという割合だけ右辺に移動しているので
$CH_3COOH $はC(1ーα）となりますね。

つまり最終的には

となるわけです。

記事中で解説したように電離定数は

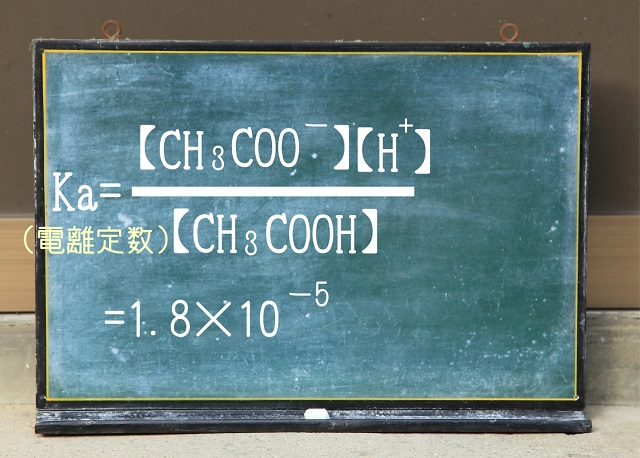
でしたね。

を代入していきます。

すると
Ka＝Cα×Cα/C(1-α）
となりますね。

上記式で分子にCが2つあって分母にCが1つあるので
１つCを消せますね。

よって
Ka＝$Cα^{２} $/(1ーα）
となりますね。

$CH_3COOH $⇔$CH_3COO^{ー} $＋$H^{＋} $

そしてさっきもいったように酢酸の場合、
兵隊さんが100人右辺に行っても
臆病だから99人は左辺に戻って行ってしまうわけです。

なのでαはだいたい１％（＝0.01）です。

ということで
Ka＝$Cα^{２} $/(1ーα）
でしたから
分母の（１－α）＝１となります。
だってαが0.01だから１－0.01＝0.99≒1
ですからね。

たとえばあなたの財布に10万円はいっていたとしましょう。
そして100円のジュースを買ったとします。
この場合、あなたの財布にはほぼ10万円ですよね。
これと同じような話です。

話を元に戻します。

Ka＝$Cα^{２} $/(1ーα）
でαが0.01だから分母はほぼ１なので
Ka≒$Cα^{２} $
となります。

Ka≒$Cα^{２} $
を変形すると
α＝$\sqrt{Ka/C} $
となります。

ここで確認しておいてほしいことがあります。
上記式から
もし濃度が小さい（Cが小さい）とαは大きくなりますね。
つまり薄くなると電離度は大きくなるってことです。
逆に濃くなると電離度は下がります。

なので濃度によって電離度は変化するということですね。

ということです。

ところでここではｐHを求めるんでしたね。
ｐHは水素イオン濃度【$H^{＋} $】の数字が必要です。
また、【$H^{＋} $】はCαでしたね。

すると、α＝$\sqrt{Ka/C} $で
酢酸濃度は問題文より0.18でしたし、
電離定数は記事中で解説しましたが1.8×$10^{-5} $(mol/L)ですから
α＝$\sqrt{Ka/C} $のルートの中は
1.8×$10^{-5} $/0.18
となりますね。

割り算するとルートの中は1.0×$10^{-４} $となります。

ではα＝$\sqrt{Ka/C} $のルートの中にある1.0×$10^{-４} $を
外に出しましょう。

すると電離度α＝1.0×$10^{-２} $（＝0.01＝１％）となります。
ということでちょうど１％だとわかりますね。
これで電離度は1％だと答えが出ました。

水素イオン濃度【$H^{＋} $】＝Cα
でα＝$\sqrt{Ka/C} $なので
【$H^{＋} $】＝Cαのαに$\sqrt{Ka/C} $を代入すると
【$H^{＋} $】＝$\sqrt{CKa} $となりますね。

【$H^{＋} $】＝Cα=0.18(mol/L)×1.0×$10^{-２} $
＝18×$10^{-４} $
となります。

ｐH=ー$log_{ 10 } [H+] $でしたね。

[H+] に18×$10^{-４} $を代入しましょう。
ｐH=４ー$log_{ 10 } ２ $ー２$log_{ 10 } ３ $
ここで$log_{ 10 } ２ $＝0.30、$log_{ 10 } ３ $=0.48なので
ｐH=４－0.30ー２×0.48＝2.74
とｐHが2.74だとわかりました。

以上で解説を終わります。