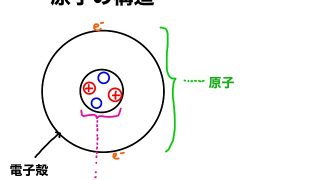
今回の記事では濃度平衡定数Kcと圧平衡定数Kpはどんな時に等しくなるのか?
わかりやすく解説します。
濃度平衡定数Kcと圧平衡定数Kpが等しくなる条件
まず質量作用の法則、すなわち平衡定数について解説します。
すごく大切ですよ。
前回の記事ではこちらの式について解説しました。
(可逆反応)
上記反応式の詳しい解説はこちらでしています。
⇒化学平衡についてわかりやすく解説
で、濃度平衡定数Kcですが。
左辺は分母で右辺は分子になります。
$2HI $の係数の2は2乗になります。
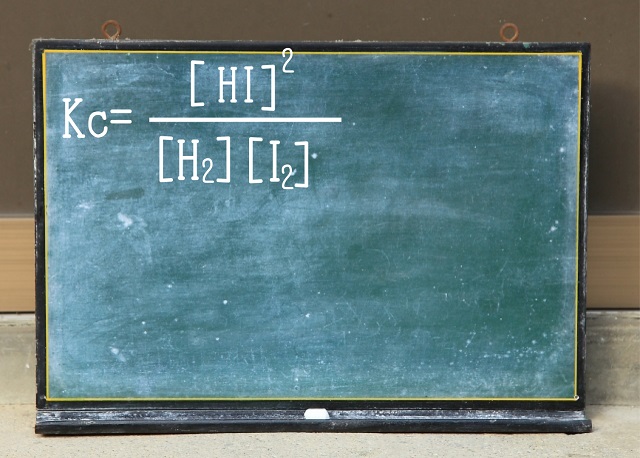
上記濃度平衡定数Kcの式は化学で大学受験をする方だったら
書けるようにしておいた方が良いと思います。
パッと見て、左辺($H_2 $+$I_2 $(気体))は分母になっていて
右辺($2HI $)は分子になっていて、係数の2が2乗になっているということが
書ければ問題ありません。
ちなみに濃厚平衡定数Kcの『c』はおまけ、添え字です。
濃度を英語でconcentrationと書きます。
このconcentrationのcがKcのcになっているわけですね。
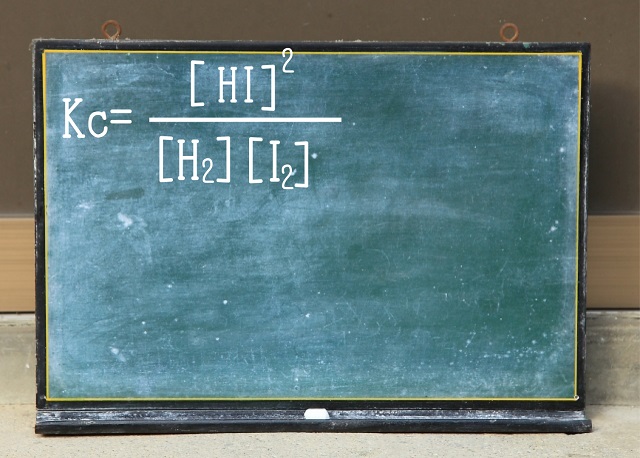
また上記式は当然ですが、濃度を表していますが
前回の記事でも反応速度で同じような式を書きましたね。
$V_1 $とか$V_2 $とかのやつです。
前回の記事はこちらです。
⇒化学平衡についてわかりやすく解説
化学平衡とは
$V_1 $(正反応)=$V_2 $(逆反応)。
つまり、正反応と逆反応の反応速度が等しいこと。
見かけ上反応が静止している。
正反応は右向き、逆反応は左向きの反応のこと。
$H_2 $+$I_2 $(気体)⇒$2HI $なら正反応
$H_2 $+$I_2 $(気体)←$2HI $なら逆反応
前回の記事を前提に話を進めていきますと
$V_1 $=$V_2 $でしたね。
$V_1 $=$V_2 $だから速度定数Kを使って$K_2 $分の$K_1 $と表します。
なので以下のような式になります。
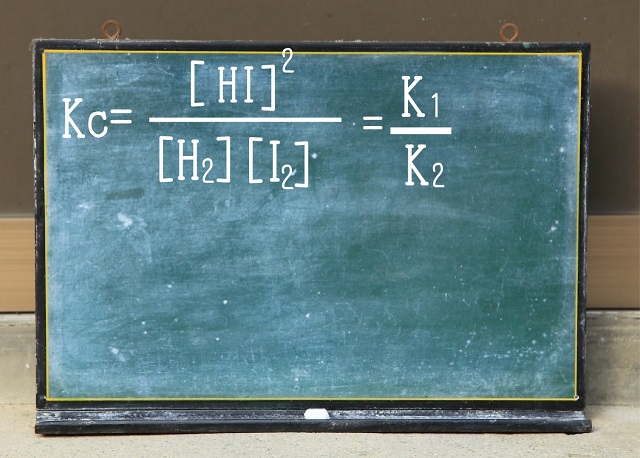
ピンときませんか?
たすき掛けするとわかりますよ。

たすき掛けすると
$V_1 $=$k_1 $【$H_2 $】【$I_2 $】
$V_2 $(逆反応)=$k_2 $【$HI $$】^{2} $
となりますね。
これは前回解説した式と同じになりますね。
確認出来たら納得しやすいですよね。
こんな感じで速度定数を使って変形することもできます。
前回の記事はこちらです。
⇒化学平衡についてわかりやすく解説
ここまでは濃度を使って書いたので濃度平衡定数ですが、
分圧を使って表す方法もあります。
これを圧平衡定数といいます。
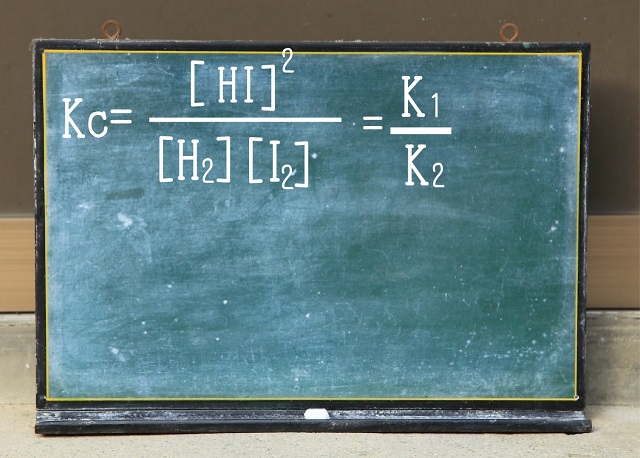
上記式を変形してみましょう。
理想気体の状態方程式を思い出してくださいね。
PV=nRT
P=圧力
n=物質量(mol)
V=気体の体積(L)
R=気体定数(0.082)
T=温度(K)
理想気体の状態方程式はこちらでも解説しています。
・ヘンリーの法則についてわかりやすく解説
上記式を変形してみましょう。
$\frac{n}{V} $=$\frac{P}{RT} $
とすることができますね。
たすき掛けすると、PV=nRTに戻りますから
問題ありませんね。
ところで変形した式の左辺$\frac{n}{V} $はmol/L(モルパーリットル)です。
nはモルでVはリットルですからね。
これは【$H_2 $】【$I_2 $】$k_2 $【$HI $$】^{2} $の【】の式のことです。
この【】の式は$\frac{P}{RT} $に置き換えることができるわけですね。
$\frac{n}{V} $=$\frac{P}{RT} $
より【】の式の$\frac{n}{V} $は$\frac{P}{RT} $とイコールの関係にありますからね。
モル濃度について詳しく知りたい方はこちら
・モル濃度の簡単な求め方についてわかりやすく解説
・モル濃度とは?わかりやすく解説
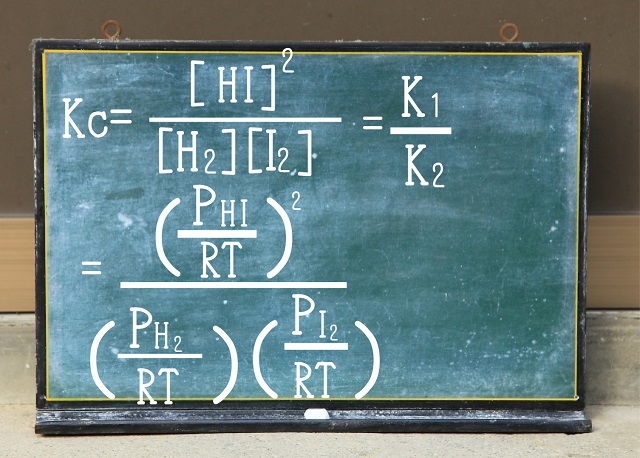
つまり、上記式のように変形できるわけですね。
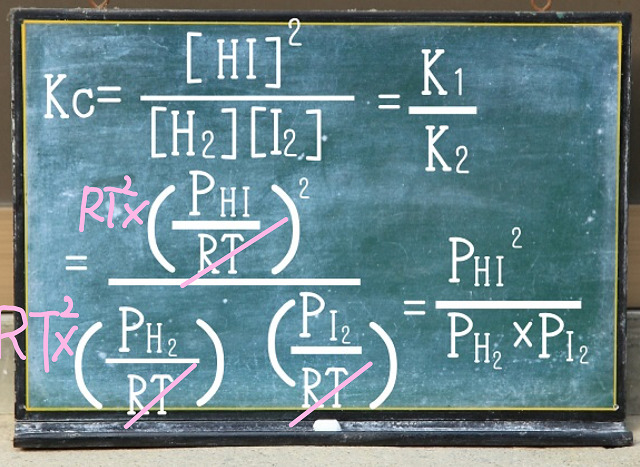
となると分母分子にRTの2乗をかけることでRTを消すことができますね。
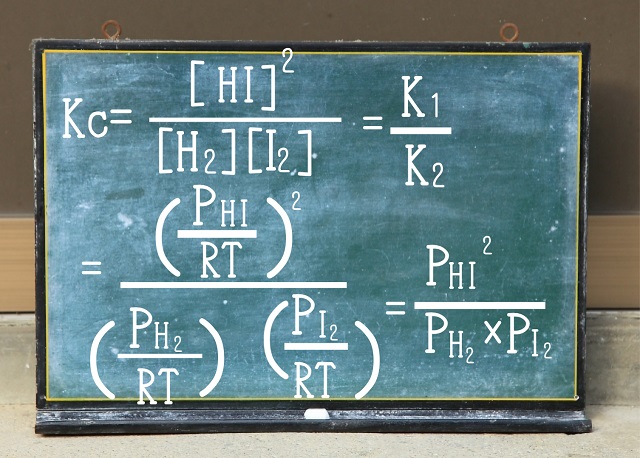
なので、ヨウ化水素($2HI $)の場合に『限った』話ですが、
きれいにRTが分母と分子で消えます。
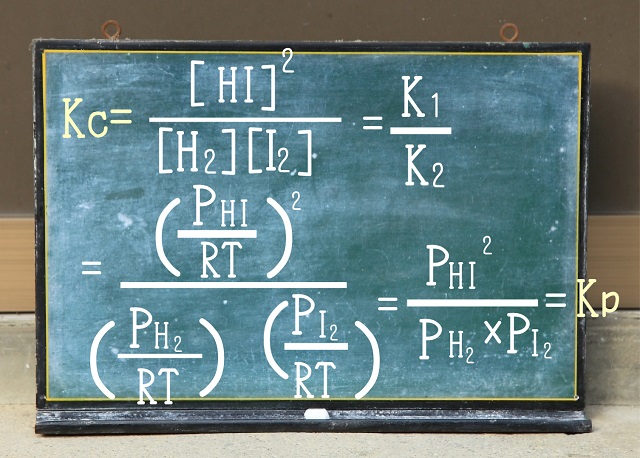
その結果、濃度平衡定数($K_c $)と圧平衡定数$K_p $は等しくなります。
こんな感じで理想気体の状態方程式を利用すれば、
mol/Lである$\frac{n}{V} $を$\frac{P}{RT} $に置き換えることによって
濃度平衡定数($K_c $)と圧平衡定数$K_p $がイコールになることを導くことができます。
濃度平衡定数($K_c $)と圧平衡定数$K_p $って何の関係もないって
思っている方もいるかもしれませんね。
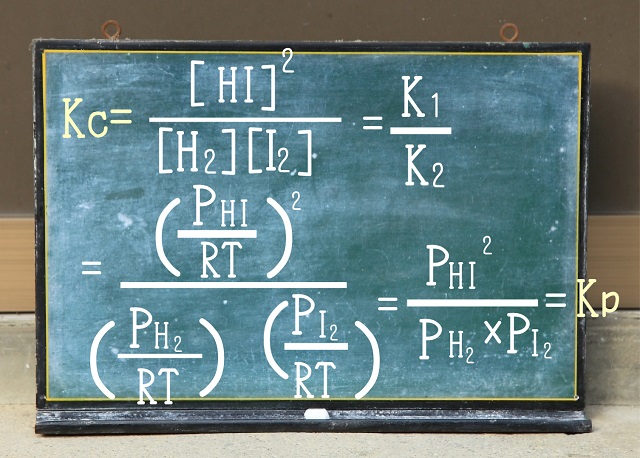
でも、上記式からわかるように
濃度平衡定数($K_c $)と圧平衡定数$K_p $は親戚同士みたいな関係なんですね。
今回扱った濃度平衡定数($K_c $)と圧平衡定数$K_p $は両方とも温度だけの関数です。
逆にいうと温度が一定なら、一定の値になります。
温度が変化すれば値が変化するものを温度だけの関数といいますからね。
ややこしかったらすみません。
以上で解説を終わります。