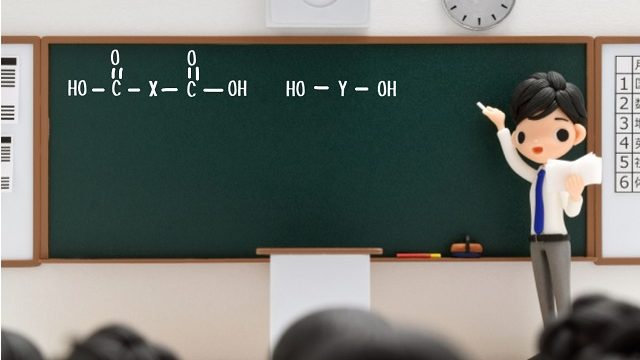※アフィリエイト広告を利用しています

化学

異性体とは？【有機化学必須知識】

 
異性体とは 化学

今回の記事では有機化学の授業で登場する異性体とは何か、
わかりやすく解説します。

スポンサードリンク




異性体とは？【化学】

異性体とは分子式が同じだけど、
分子の構造が違うために、性質が違ってくる物質同士のことです。

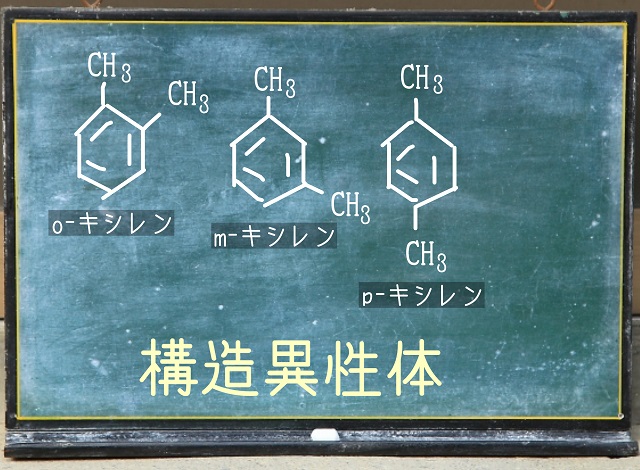
構造異性体

たとえば上記画像をご覧ください。
3つともベンゼン環に$CH_3 $が2つついていて
分子式は同じになります。
⇒組成式・分子式・示性式の違いについてわかりやすく解説
でも、ベンゼン環に$CH_3 $がつく位置が違うために性質が違ってくるのです。
こういうのが異性体（構造異性体）の一例です。

こんな感じで異性体とは同じ分子式だけど物が違うもののことです。
物が違うことで融点や沸点や化学的な反応性などが変わる場合がありますが、
そういうのは互いに異性体といいます。

ところで

異性体には

・構造異性体
・立体異性体

があります。

スポンサードリンク




構造異性体とは？

構造異性体とは何でしょう？
いろんなパターンがありますが、炭素骨格が異なるものとしてブタンとメチルプロパンが有名です。
炭素が4つ直列につながっているのがブタンで、
メチルプロパンというのは枝があります。

構造異性体

メチルプロパンの場合、2番目の炭素に$CH_3 $という枝がついていますよね。
この$CH_3 $はメチル基という構造で、要するに枝になっているわけです。
3つの炭素がつながっている2番目に枝がついています。
こんな感じで枝を持った構造をしているのがメチルプロパンです。

ブタンとメチルプロパンって同じ分子式ですよね。
原子の数は同じですよね。
炭素は4つあって水素が10個あるという点は同じです。

$C_4H_10 $という同じ分子式で書けるけど
構造が違う、これが構造異性体です。

不飽和結合の位置が違う構造異性体

他にも不飽和結合の位置が違う構造異性体もあります。

不飽和結合の位置が違う構造異性体として

・1－ブテン（$H_2C＝CHーCH_2ーCH_3 $）
・2－ブテン（$H_3CーCH＝CH_2ーCH_3 $）

があります。

1－ブテンと2－ブテンでは分子式は同じですが、
二重結合の場所が違います。

どちらも分子式は$C_4H_8 $です。
同じ分子式ではあるのですが、二重結合の位置が違うから物が異なる、
これも構造異性体になります。

官能基の位置が違う構造異性体

官能基の位置が違う
分子式は$C_3H_8O $

上記の２－プロパノールのOH部分をご覧ください。
このOH部分はヒドロキシ基というアルコールというのを特徴づける構造になっています。

そして１－プロパノールというのは端の炭素CにOHがついていますね。
これに対して２－プロパノールは2番目の炭素にOHがついていますよね。
ヒドロキシ基の場所が違うだけで、分子式は$C_3H_8O $と同じだけど
性質に違いが出てくるので構造異性体の一種です。

官能基の種類が違う構造異性体

官能基の種類が違う構造異性体として

・エタノール
・ジメチルエーテル

が有名です。

エタノールもジエチルエーテルもどちらも分子式は$C_2H_6O $と同じです。
エタノール（$CH_3ーCH_2ーOH $）の『OH』部分はヒドロキシ基です。
でも、ジメチルエーテル（$CH_3ーOーCH_3 $）の『ーOー』はエーテル結合という結合で
ヒドロキシ基とは違った官能基です。

エーテル結合はの『ーOー』両サイドに炭化水素がついた結合です。
OHのヒドロキシ基はアルコールでOはエーテルで種類が違います。
だから融点や沸点も違ってきます。

分子式は同じだけど、アルコールというグループとエーテルというグループという
違うグループに分かれるので構造異性体に該当します。

構造異性体まとめ

構造異性体は全部同じ分子式です。

ブタンとメチルプロパンは分子式は$C_4H_10 $です。
同じ分子式ですが、枝があるかないかで物が異なってきます。

次に1－ブテンと2－ブテンはどちらも分子式は$C_4H_8 $と同じだけど、
二重結合の場所が異なるために名前や性質が変わってきます。

それから２－プロパノールと１－プロパノールでは
同じ分子式だけどヒドロキシ基の場所が2番目か端かの違いで構造が違ってきます。

エタノールもジエチルエーテルはヒドロキシ基かエーテル結合かの違いで
種類が違ってきます。

以上はどれも構造異性体の具体例です。

スポンサードリンク




立体異性体とは？

異性体には

・構造異性体
・立体異性体

があるのでした。

立体異性体とは略式（簡略）の構造式で書くとまったく同じ。
でも、立体的に見てみるとものが違うものが立体異性体です。
⇒簡略構造式の書き方ルールについてわかりやすく解説

立体異性体には

・幾何異性体
・光学異性体

があります。

幾何異性体とは？

まず幾何異性体からみていきましょう。

2－ブテンを簡略構造式で書くと$H_3CーCH＝CH_2ーCH_3 $となります。
⇒簡略構造式の書き方ルールについてわかりやすく解説

2－ブテンには立体的には見ると別物に見える立体異性体があります。

具体的には

2ーブテンには

・トランスー２ブテン
・シスー２ーブテン

の2つの立体異性体（幾何異性体）があります。

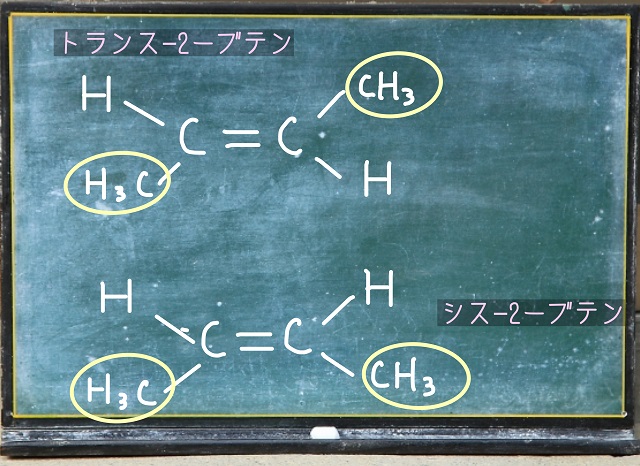
幾何異性体

上記画像をご覧ください。
トランスー２ブテンもシスー２ブテンも
黄色い〇で囲んでいるところは$CH_3 $（メチル基）です。
トランスー２ブテンは$CH_3 $（メチル基）が対角線方向に存在してますよね。
これに対してシスー２ブテンは$CH_3 $（メチル基）が同じ側に出ています。

シスー２ブテンとトランスー２ブテンは同じものでしょうか？
異なるものでしょうか？
この2つの構造って厳密にはピッタリと重なることはありません。

たとえば、
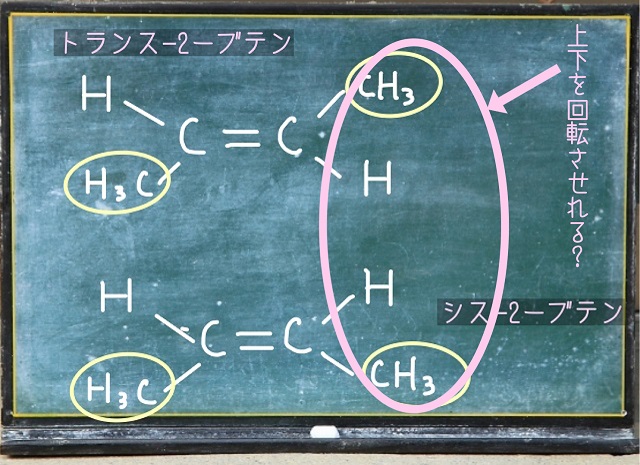
上下に回転

上記画像のようにシスー２ブテンとトランスー２ブテンのどちらかを左側を固定した状態で
右側のピンクで囲っている部分をくるっと回転させることができるでしょうか？
もし回転させることができるなら、シスー２ブテンとトランスー２ブテンは完全に一致しますね。
シスー２ーブテンだけを回転させることができるなら、トランス２ーブテンになりますし
トランスー２ブテンだけを回転させることができるなら、シスー２ブテンになります。

でも、上下って入れ替わりません。
回転しません。C=C部分が二重結合だからです。
C-Cと単結合なら回転できるけど、二重結合（C=C)は回転できないんでしたね。
これは前回の記事で詳しく解説していますので気になる方はこちらをご覧ください。
⇒炭素間の結合距離と回転の可否についてわかりやすく解説

回転しないからシスー２ブテンとトランスー２ブテンは厳密にいうと同じものではないということです。
二重結合が回転できないことによって登場する異性体、これが幾何異性体です。

幾何異性体とは炭素間の二重結合が回転できないという性質があるために存在する異性体のことです。

幾何異性体

そして対角線方向に同じものが出ている場合がトランスで
同じものが同じ側に出ている場合がシスとなります。
だからシストランス異性体と言われたりします。

簡略構造式にすると同じだけど、
幾何的に考えてみると別物ということで幾何異性体といいます。

光学異性体とは？

4方向すべて異なるものが単結合で結合した炭素のことを不斉炭素原子といいます。

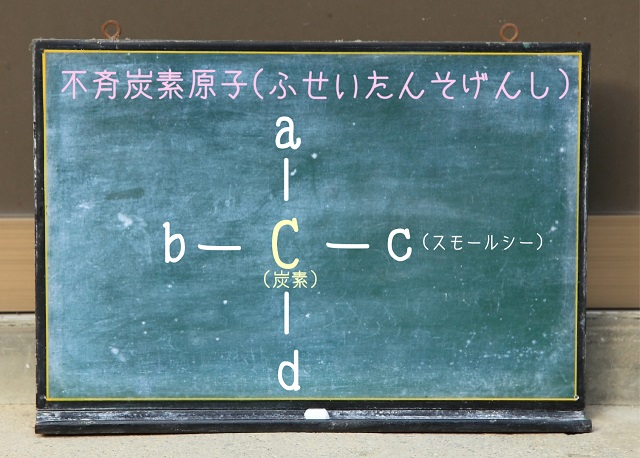
不斉炭素原子

上記画像をご覧ください。
中心のC（炭素）の周りにa,b,c,dという4つ全部ことなるものが結合していますね。
この場合の中心C(炭素）を不斉炭素原子といいます。

「だからなんだよ！」って突っ込まれそうな気がします（苦笑）。

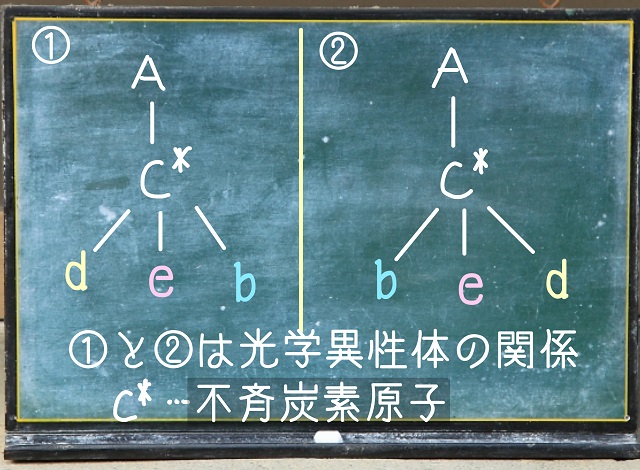
光学異性体

上記画像をご覧ください。
⓵も⓶も4つ全部違う原子がくっついています。

⓵と⓶の間に鏡を置いたとしましょう。
鏡を置いたときにうつる像を鏡像（きょうぞう）といいます。
⓵と⓶をよくみると鏡像の関係になっていますね。

では

光学異性体

⓵と⓶を重ね合わせたら重なるのでしょうか？
Aとeは重なります。
でも、bとdは重なりません。

光学異性体

つまり、持っている構造はまったく同じ、分子式もまったく同じなのに
立体的に見てみると⓵と⓶は同じものではないということです。
もし無理やりｂとｄを合わせたとしたら
今度はＡとeが重なりません。

だから⓵と⓶は別物です。
これを互いに光学異性体といいます。

よく左手と右手の関係といわれます。

左手と右手

左手と右手の間に鏡があったとしましょう。

鏡

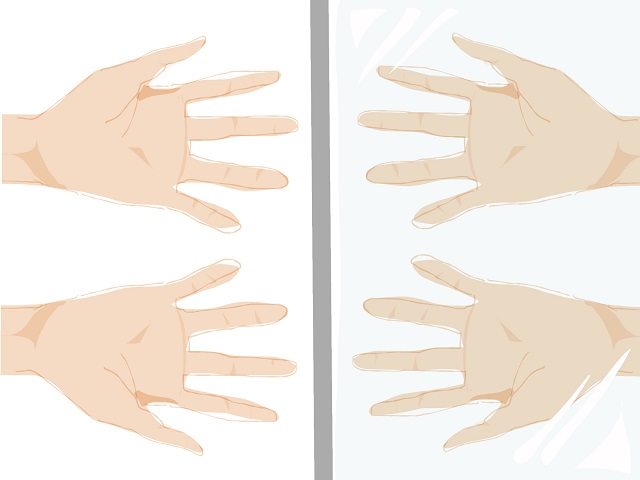
左手と右手はぴったりと重なり合いません。
これが鏡像の関係です。

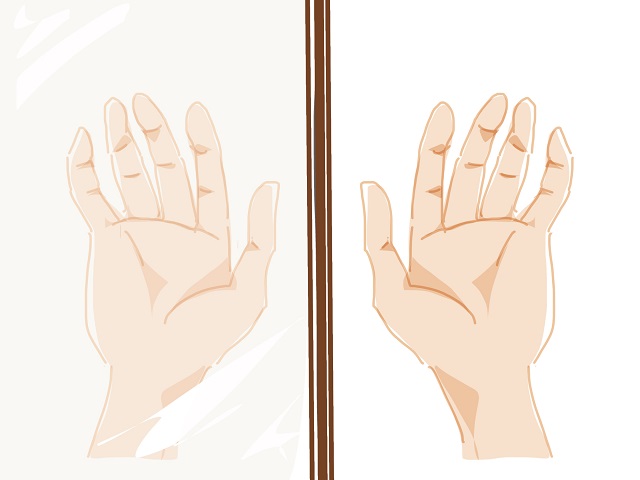
鏡像の関係

上記画像で左側に映っている手と右側に映っている手を
そのまま重ね合わせても、ぴったりと重なり合いませんよね。
これが鏡像の関係です。

不斉炭素原子という4方向すべて異なるものが結合した炭素があると
鏡像異性体（光学異性体）というものが出てきます。

だから光学異性体だと言えるためには
4方向すべて異なるものがついた不斉炭素原子です。
不斉炭素原子があると鏡像異性体（光学異性体）が出てきます。

逆に不斉炭素原子でなければ光学異性体にはなりません。
炭素の周りに2つ同じものが存在していたら
鏡像の関係にならないからです。左右で同じ構造になってしまいますから。

今回の記事では簡単に異性体とは何か、解説しました。
今後の記事でもう少し詳しく異性体について説明していきますので
よろしくお願いします。

スポンサードリンク




化学 異性体とは
関連記事