※アフィリエイト広告を利用しています

化学

シャルルの法則が当てはまる身近な例とは？

  /
シャルルの法則

前回の記事ではボイルの法則について解説しました。

ボイルの法則は
P=$\frac{定数}{V} $

変形すると
PV=一定

となる法則でしたね。

あわせて読みたい

前回の記事はこちらです。
・ボイルの法則についてわかりやすく解説

ボイルの法則は1662年に発表されました。

今回の記事ではシャルルの法則について
図を使ってわかりやすく解説した後、
シャルルの法則の身近な例について解説したいと思います。

スポンサードリンク




シャルルの法則とは？

シャルルの法則とは

圧力（P)と物質量（n）が一定のもとで
体積（V)と温度（T)が比例する

という法則のことです。

前回の記事のようにピストン型容器での話です。
今、上からＰ（atm)の圧力をかけたとしましょう。
中には気体分子が入っていて、温度はT(k）としましょう。

体積はV(L)だったとしましょう。

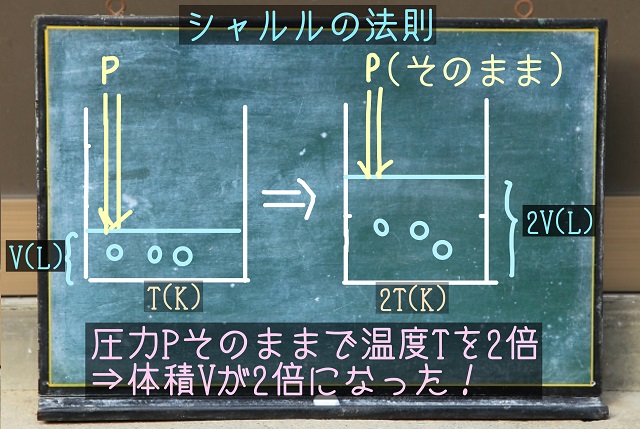
シャルルの法則

この状況から絶対温度を2倍に引き上げます。
加熱するという意味です。
上からの圧力Pはそのままで2倍の絶対温度を与えると
体積は2倍の2V(L)になるということをシャルルさんは見つけたのです。

これがシャルルの法則です。

あわせて読みたい

前回の記事はこちらです。
・ボイルの法則についてわかりやすく解説

シャルルの法則を式で表すと

V=定数×T

変形すると
$\frac{V}{T} $=一定

V:体積
T：絶対温度

と比例関係になります。

V=定数×T
は中学校で習った一次関数y=ax
と同じ感じですからね。

まとめると

シャルルの法則は絶対温度Tと体積Vが比例するという法則のこと

です。

スポンサードリンク




シャルルの法則の身近な例をご紹介します

シャルルの法則の身近な例（１）へこんだピンポン玉

シャルルの法則とは

絶対温度Tと体積Vが比例するという法則のこと

でしたね。

ではこの地球上でシャルルの法則を感じれるような
身近な例ってどこにあるのでしょうか？

たとえば、ボコッとへこんだピンポン玉があるとしましょう。
そのピンポン玉にお湯をつけると元に戻ります。

へこんだピンポン玉の中の体積は元のポンポン玉の体積よりも小さいですね。
たとえばへこんだピンポン玉の体積がVだったとしましょう。
それで部屋の温度がTだったとします。

で、へこんだピンポン玉（体積V)をお湯（部屋の温度より高いので2Tとします）につけると
体積Vのへこんだピンポン玉が元のピンポン玉（体積が2V）に戻るわけですね。
これはまさにシャルルの法則が当てはまる身近な例でしょう。

シャルルの法則の身近な例（２）ゴム風船

まずこちらの動画をご覧ください。

丸底フラスコにほんのちょっぴりの水を入れてから
バーナーの火であぶります。

すると、水が沸騰するので水蒸気に変わります。
状態変化ってやつですね。

あわせて読みたい

・状態変化とは？図を使ってわかりやすく解説
・状態変化グラフの見方・考え方をわかりやすく解説

で、丸底フラスコ内が水蒸気でいっぱいになったら火を止めます。
そして丸底フラスコの口にゴム風船をくっつけます。

すると面白い現象が起こります。
ゴム風船がフラスコの中にキュッと吸い込まれてしまうんですね。
これはどういうことでしょう？
水蒸気で満たされたフラスコでしたが、火を止めたので水蒸気が水に戻ります。
このとき体積が約1650分の1になるのです。

結果、フラスコの中が真空に近い陰圧状態になったためゴム風船が吸い込まれてしまったのです。
これはシャルルの法則的にいったら
温度が下がったから体積が減ったということができるでしょう。

次にもう一度丸底フラスコを温めます。
するとゴム風船がまた膨らみます。

これはシャルルの法則的にいったら
絶対温度が高くなったから体積が増えたためと考えることができますね。

シャルルの法則の身近な例（３）富士山

富士山

富士山の頂上ってめっちゃくちゃ寒いです。
真夏でも7℃くらいしかありません。

でも富士山のふもとだと真夏だったら30℃以上あるでしょう。

富士山に限った話ではありませんが、
地上からどんどん空に向かっていくほど、気温は下がります。

気温は

100メートル高くなるごとに0.6℃下がります。

富士山は3776mあります。
だから、約37×0.6＝22.2℃くらい富士山のふもとと頂上では違うといえるでしょう。
これは事実です。

ということはシャルルの法則から
富士山のふもとと、頂上では気体の体積も違ってくることは想像に難くありません。
シャルルの法則がわかっていたら
温度の低い富士山の頂上の方が気体の体積が小さくなる、
つまり酸素の濃度が薄くなることがわかるはずです。

もちろん富士山のふもとの方が頂上より温度が高いので
酸素は濃くなります。

もちろんエベレストは富士山よりも高山なので、
もっと酸素は薄いです。

以上でシャルルの法則の身近な例についての解説を終わります。

シャルルの法則から約30年後、
ボイルの法則、シャルルの法則の次、3つ目の法則であるアボガドロの法則が発表されます。
続きはこちら。
⇒アボガドロの法則について計算問題を使いながらわかりやすく解説

スポンサードリンク




シャルルの法則 例
関連記事