・ボイルの法則
・シャルルの法則
・アボガドロの法則
という3つの気体法則ついて解説してきました。
ではここまで解説した3つの気体法則を理解している前提で
理想気体の状態方程式を図を使ってわかりやすく導出してみたいと思います。
ボイルの法則、シャルルの法則、アボガドロの法則を組み合わせていきますよ。
(理想)気体の状態方程式の前段階|ボイルシャルルの法則を導出してみる!
ではまず以下の図をご覧ください。
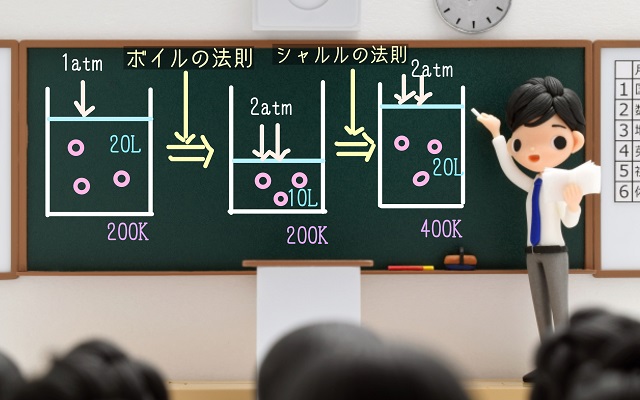
上記図の一番左側をご覧ください。
200K(ケルビン)という温度で中に気体分子が入っているとします。
上から1atmという圧力を加えます。
上記図の容器はピストン型容器とします。
ピストン型容器の特徴は上からかけた圧力と容器内の圧力はイコールになります。
バイク弁当のピストン型容器、頭のバルブ避け部分の形状がちゃんと吸気と排気で形変えてあるのな。 pic.twitter.com/l346Hb2EmJ
— くれは (@908kureha) February 1, 2021
なので容器内の気体の圧力も1atmになります。
このとき、中の体積が20Lだったとしましょう。

ではボイルの法則で考えてみましょう。
上記図の真ん中をご覧ください。
上からかける圧力を2倍の2atmにしてみましょう。
ボイルの法則により、中の体積は2分の1である10Lになりますね。
ボイルの法則についてはこちらで解説しています。
・ボイルの法則についてわかりやすく解説
次にシャルルの法則を利用してみましょう。

上記図の一番右側をご覧ください。
左側と真ん中の図では200K(ケルビン)でした。
一番右側では圧力P気体分子の数を変えずに400Kにかえてみます。
絶対温度を2倍にするということです。
すると体積が2倍の20Lになります。
シャルルの法則では絶対温度に比例する形で容器の大きさは大きくなります。
絶対温度が2倍になったから中の体積が2倍になったわけです。
これがシャルルの法則です。
シャルルの法則についてはこちらで解説しています。
・シャルルの法則が当てはまる身近な例とは?

もう1度上記図をご覧ください。
・一番左は1atm、20L、200K
・真ん中は2atm、10L、200K
・一番右は2atm、20L、400K
でした。
上記図の数字に共通する規則性分かりますか?
圧力と体積をかけた値を絶対温度で割ります。
すると3つとも同じ数字になりますね。
・一番左は1atm×20L÷200K=0.1
・真ん中は2atm×10L÷200K=0.1
・一番右は2atm×20L÷400K=0.1
とすべて同じ数字になりましたね。
圧力×体積÷絶対温度が一定値になることが
ボイルの法則とシャルルの法則を組み合わせることで導出することができますね。
PV/T=一定
だとわかります。
PV/T=一定
は、ボイルの法則とシャルルの法則を組み合わせて出てくる式なので
ボイルシャルルの法則って言います。
ボイルシャルルの法則は大学受験でも頻出ですが、
ここまで解説しきた流れで導出することができます。
次に1811年に発表されたアボガドロの法則を組み合わせて(理想)気体の状態方程式を導出してきましょう。
(理想)気体の状態方程式を導出してみる!
以下の図をご覧ください。
先ほどと同様、ピストン型容器です。
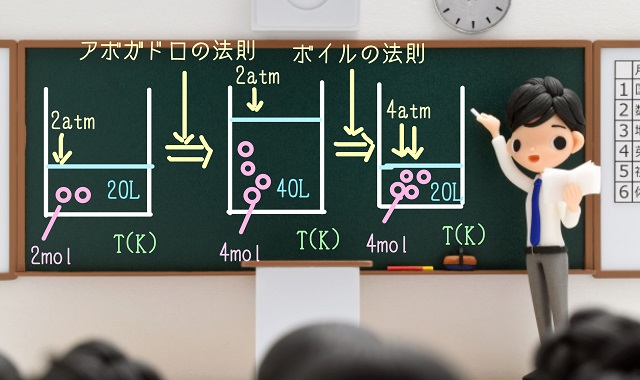
上記図の一番左をご覧ください。
アボガドロの法則なのでモル数も登場します。
2molの気体がT(ケルビン)という温度で封入されているとします。
上から2あtmという圧力をかけています。
ピストン型容器なので中の圧力も2atmになります。
ここはそういうものだと思ってください。
そしてこのときの中の体積が20Lだとしますね。
ここから中の気体のモル数(物質量)を2倍の4molに増やしてみましょう。
これがアボガドロの法則ですね。

上記図の真ん中をご覧ください。
温度や圧力を変えずにモル数が2倍に4molになりました。
気体の物質量だけ2倍に増やしました。
そうすると中の体積はアボガドロの法則により
2倍の40Lになります。
アボガドロの法則についてはこちらで解説しています。
・アボガドロの法則について計算問題を使いながらわかりやすく解説
そしてここからもう1度ボイルの法則が反映される場合を
考えてみましょう。

上記図の一番右をご覧ください。
4molのままモル数変化なし、温度もT(ケルビン)のまま。
上からの圧力だけ2atmを4atmの2倍にしたとしましょう。
すると体積は半分の20Lになりますね。
ボイルの法則についてはこちらで解説しています。
・ボイルの法則についてわかりやすく解説

上記図から規則性を考えてみましょう。
・一番左は2atm、20L、2mol、T(ケルビン)
・真ん中は2atm、40L、4mol、T(ケルビン)
・一番右は4atm、20L、4mol、T(ケルビン)
圧力と体積を掛け算してそれをモルと絶対温度で割った値は
3つとも同じになります。
・一番左は(2atm×20L)÷(2mol×T)=20/T
・真ん中は(2atm×40L)÷(4mol×T)=20/T
・一番右は(4atm×20L)÷(4mol×T)=20/T
とどれも20/Tと一定の値になっていますね。
モル数をn圧力をP、絶対温度をT、体積をVとすると、
PV/nT=一定(R)
となりますね。
PV/nT=一定
の一定はRと置きます。
上記式を変形しましょう。
PV/nT=Rを変形すると
PV=nRT(理想気体の状態方程式)
となり、導出することができました。
PV=nRT
という式こそが理想気体の状態方程式ですね。
ちなみにRは気体定数といいます。
理想気体の状態方程式が完成するのに約150年かかっています。
ボイルの法則、シャルルの法則、アボガドロの法則を組み合わせることで
理想気体の状態方程式を導出することができます。
高校の授業だと理想気体の状態方程式PV=nRTが存在する前提で
ボイルの法則、シャルルの法則、アボガドロの法則を
説明していたと思います。
私が高校生時代もそうでした。
⇒当ブログ管理人のプロフィール
これは説明できて当然でしょう。
なぜならボイルの法則、シャルルの法則、アボガドロの法則を組み合わせて
理想気体の状態方程式が導出されているわけですからね。
逆も導出可能でしょう。
でも理想気体の状態方程式は
ボイルの法則、シャルルの法則、アボガドロの法則があったから
導出できた式です。
以上で解説を終わります。