※アフィリエイト広告を利用しています

化学

原子量・分子量・式量の違いについてわかりやすく解説

  /
原子量 分子量 式量 違い

この記事では原子量・分子量・式量の違いについてわかりやすく解説していきます。

スポンサードリンク




原子量・分子量・式量の違い

原子量、分子量、式量の違いを理解するために
実際に原子量、分子量、式量の求め方（計算方法）について
解説していきます。

原子量の求め方

原子量の求め方について解説します。
例題として$Cu $（銅）を使っていきますね。

銅原子を調べてみると質量数の異なるものが見つかります。
質量数についてはこちらの記事で解説しています。
⇒原子量と質量数の違いについてわかりやすく解説

銅原子には

・質量数が63の${}^{ 63 } Cu $
・質量数が65の${}^{ 65 } Cu $

があります。

銅原子を100個拾ってきたら
たいたい70個くらいが質量数が63の${}^{ 63 } Cu $で
だいたい30個くらいが質量数が65の${}^{ 65 } Cu $です。

別の表現をすると質量数が63の軽い銅と
質量数が65の重い銅です。

この軽い銅と重い銅の体重を昔の人は調べていて
この体重を相対質量といいます。
銅の原子番号が同じで元素記号が同じ。
でも質量数が異なるもの同士を同位体といいます。

あわせて読みたい

・同位体とは？塩素と炭素を例に分かりやすく解説

銅の同位体には質量数が63の軽い銅と
質量数が65の重い銅があるということです。

そして軽い銅の方の体重（相対質量）が63で
重い方の銅の体重（相対質量）は65だということです。

銅の質量数と相対質量の関係

・${}^{ 63 } Cu $（質量数63）⇒相対質量も63
・${}^{ 65 } Cu $（質量数65）⇒相対質量も65

でした。

銅に関して言えば
質量数と相対質量が完全に一致しています。
ただ問題によっては少し63からちょっとずれる。
65からちょっとずれるみたいな感じ数字が与えられることもあります。
なので質量数とほぼ同じ値になるか、問題によっては
この記事のようにピタッと質量数と相対質量が一致するように与えられることもあります。

とにかく相対質量は体重くらいに考えましょう。
そして銅には軽い銅と重い銅があって軽い銅は69％、
100個中69個の割合で存在します。

そして重い銅は100個中31個の割合で存在するわけです。
もっとわかりやすくいうと
軽い銅が69人いて重い銅が31人いるみたいな感じです。
私たちは通常、軽い人と重い人みたいな感じで
区別しませんよね。
たとえば小学校のクラスで重い人と軽い人でクラス分けしたりしませんよね。
もし体重で分けるとしたらボクシングとか柔道とか
そういった世界くらいじゃないでしょうか。

だから重い銅、軽い銅って区別せずに単純に銅っていうわけですよ。
そこで軽い銅と重い銅をごちゃまぜにして平均を考えることになります。

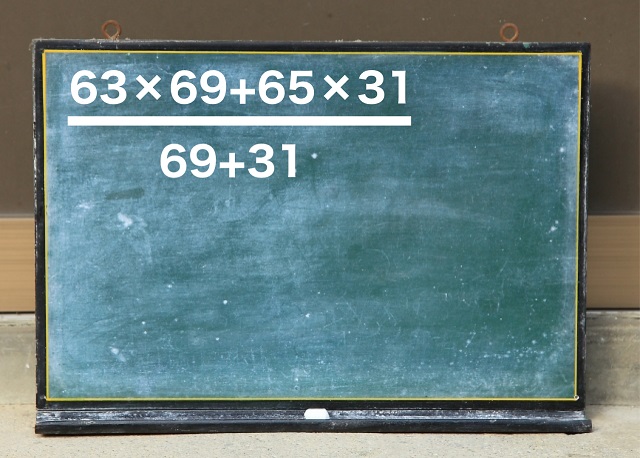
原子量の計算式の途中

63の体重の人が69人、65の体重の人が31人いるって考えます。
63×69＋65×31という式になります。
この式は全員の体重の合計を意味しますね。

この全員の合計体重を全員の人数（69＋31＝100人）で割れば
平均体重が出ますね。
それが上の式です。

計算式

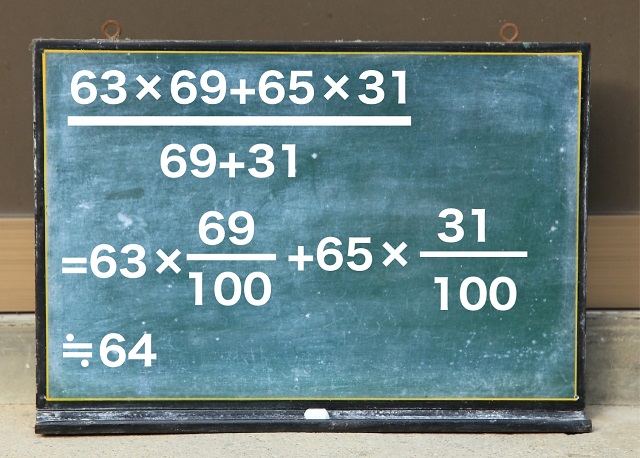
この平均の式ですが
分母は100になりますから、上記図のように
式を崩したほうが計算しやすくなりますよ。
計算結果は63.62になって約64になります。

こんな感じで軽い銅と重い銅を区別せずに
原子量を調べるときは相対質量の平均を考えるということになります。
これが原子量です。

次に分子量について解説しますね。

分子量の求め方

分子って覚えていますか？
$H_2 $とか$H_2O $などいろいろありますよね。
こんな感じで原子が何個かくっついて出来上がった塊が分子です。

分子量とは分子を構成している原子の原子量の合計のことです。
これで原子量と分子量の違いがわかったと思います。

たとえば$H_2 $。
軽い水素H、重い水素Ｈを区別していません。
ただ単に$H_2 $って書いてあるので
先ほど原子量のところで解説した平均の考え方を利用します。
先ほどと同じように計算すると水素だと1.0くらいになります。
この1.0は問題文中に書かれているはず。
なので暗記は不要です。

話を戻して$H_2 $の場合は原子量1.0の水素が2個くっついています。
だから1.0×2＝2.0と分子量を求めることができます。

$H_2O $の場合は水素の原子量が1.0で、
酸素の原子量は16と問題文中に普通書かれています。

なので$H_2O $の場合は水素1.0×2個＋酸素16×1＝18
よって$H_2O $の分子量は18となります。

こんな感じで分子量を計算していくことになります。
分子量は原子量の合計だということです。

分子量は

原子量の合計

ということになります。

式量の求め方

式量は分子量に似ています。
だから原子量と式量はまったく違います。
式量って何でしょう？

イオン結合
たとえば食塩（NaCl）。
イオン結合のところで解説しましたが、
食塩は上記図のように$Na^{＋} $と$Cl^{ー} $が
ずっとつながっているわけです。
⇒イオン結合の特徴についてわかりやすく解説

そこで繰り返しの最小単位を考えてみましょう。
$Na^{＋} $と$Cl^{ー} $が繰り返されていることがわかります。
これを前回解説したように組成式といいます。
⇒構造式・示性式・分子式・組成式の違いを酢酸を例にわかりやすく解説

$Na^{＋} $200、$Cl^{ー} $200みたいに
存在する数で書かずに約分して
$Na^{＋} $：$Cl^{ー} $＝１：１の比で
くっついているということでシンプルにNaClと書くわけです。

大丈夫でしょうか？
イオン結合
実際のNaClは上記図のようなのが無限に連なっているんです。
でもそれじゃ、表現しきれないので組成式としてNaClと表現しているんです。
こんな形で組成式で表すものについては原子量を足し合わせます。
これを式量といいます。

分子量と式量の違い

・分子量は分子式で表される原子量の合計
・式量は組成式で表される原子量の合計

ということです。

Naの原子量は23と与えられることが多いです。
Clの原子量は35.5と与えられることが多いです。

よって組成式NaClの場合は23＋35.5＝58.5
となるので式量は58.5だということがわかります。

こんな感じなので分子量、式量については化学式を見ながら
原子量の合計を調べていけばOKです。

今回の記事は以上になります。
もし組成式と分子式の違いが分からないようでしたら
こちらの記事をご覧ください。
⇒構造式・示性式・分子式・組成式の違いを酢酸を例にわかりやすく解説

スポンサードリンク




分子量 原子量 式量 違い
関連記事